Sierpinski Carpet Relatives

Description

The construction of these fractals is motivated by the web page "Square divided by nine" by Robert Fathauer, part of his website on Gasket Fractals. Start with a square rotated by 45°. Divide this into 9 smaller congruent squares. If the middle square is removed and the construction is iterated on the remaining squares, the result is the Sierpinski Carpet, but rotated 45°.

rotated carpet design $rotated carpet fractal$

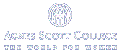
The image on the right shows the basic design of the remaining initial squares considered to have an upward orientation. But suppose the top square is removed rather than the middle square. Iterating that construction would produce a different fractal.

Top square removed Fractal when top square removed

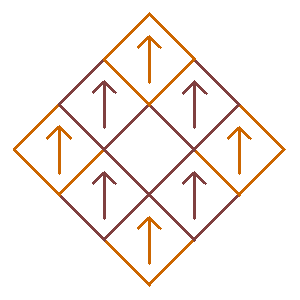
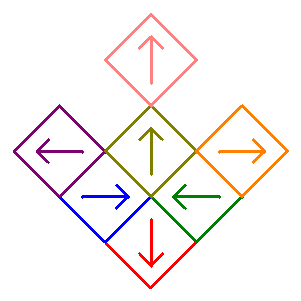
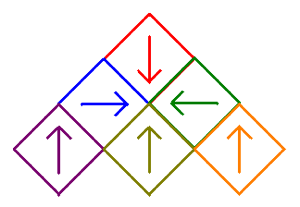
In general, we can choose to remove from 1 to 8 squares to form the basic design. In addition, however, we can also choose to rotate any of the remaining squares by 90° counterclockwise, by 180°, or by 270° counterclockwise (i.e. 90° clockwise) as that will maintain their relative positions, but change their orientation. For example, suppose only the top square is removed as before, but now the three squares in the middle row are rotated by 90°, 180°, and 270° counterclockwise respectively as illustrated in the design below along with the first four iterations. View the animation to see how the arrows are rotated during these four iterations, and view the video to see how the eight scaled hearts fill their respective squares while points are plotted using the chaos game algorithm with the IFS described below.

Deterministic
Animation

Chaos Game
Video

top square removed, with 4 squares rotated
iteration 1 iteration 2 iteration 3 iteration 4

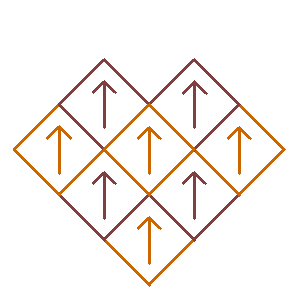
Because we are only interested in symmetric fractals, we will always require that the basic design be symmetric with respect to a vertical line through the middle. Because of this symmetry requirement, any horizontal, vertical, or diagonal reflection of a square can be represented instead by one of the four rotations of a square [Rotation Details].

Iterated
Function
System

Labeling the 9 squares from 1 to 9, bottom to top

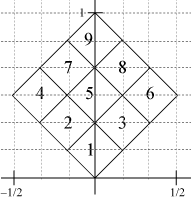Take the initial square to have diagonals of length 1 and bottom vertex at the origin. If the nine squares are labeled from 1 to 9 as shown to the right, then each of the functions corresponding to a particular square can be indexed by the same number as the triangle. This gives the nine functions below. The translation vectors are determined by how the bottom vertex of square 1 has to be moved to the bottom vertices of the other eight squares. Each gridline corresponds to 1/6.

Use the dropdown menus to chose 0°, 90°, 180°, or 270° depending on how a square is to be rotated. If a square is to be deleted, choose "Remove" from the menu. Finally, click on the "Create IFS" button. The IFS for that fractal will consist of the functions below whose indices match those of the remaining squares and for which the appropriate angle of rotation is specified.

IFS Video
Demonstration

For example, if the top square is removed (square 9) as shown in the "heart" above, and $\theta_4=90^\circ$, $\theta_5 = 180^\circ$, and $\theta_6 = 270^\circ$, then the IFS for the resulting fractal is the set $\{f_1,f_2,f_4,f_5,f_6,f_7,f_8\}$ with the corresponding rotation angles.

Index	Function	Scaling/Rotation
1.	${f_1}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {0} \\ {0} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_1$ =

2.	${f_2}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {-1/6} \\ {1/6} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_2$ =

3.	${f_3}({\bf{x}}) =\displaystyle \left[ {\begin{array}{c} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {1/6} \\ {1/6} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_3$ =

4.	${f_4}({\bf{x}}) =\displaystyle \left[ {\begin{array}{*{20}{cc}} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {-1/3} \\ {1/3} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_4$ =

5.	${f_5}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {0} \\ {1/3} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_5$ =

6.	${f_6}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {1/3} \\ {1/3} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_6$ =

7.	${f_7}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {-1/6} \\ {1/2} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_7$ =

8.	${f_8}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {1/6} \\ {1/2} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_8$ =

9.	${f_9}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {0} \\ {2/3} \\ \end{array}} \right]$	scale by 1/3, rotate by $\theta_9$ =

Naming
Convention

Each design can be labeled by a string of length 9 corresponding to the numbered position of the subsquares as shown above, with each string item representing how the corresponding subsquare is rotated or deleted.

Label	Meaning
1	Rotate 0°
2	Rotate 90°
3	Rotate 180°
4	Rotate 270°
x	Remove square

So the Sierpinski Carpet would be labeled as 111-1x1-111 (dashes added to help readability). The "heart" shaped fractal shown above would be labeled as 111-234-11x.

Similarity
Dimension

Suppose $m$ squares are removed at each iteration of the construction, where $1 \le m \le 7$ (if you remove 8 squares, leaving only one, the limit of the iteration will be a single point.) The resulting fractal is self-similar with $(9-m)$ non-overlapping copies of itself, each scaled by the factor r = 1/3. Therefore the similarity dimension, $d$, of the attractor of the IFS is the solution to

$$\sum\limits_{k = 1}^{9-m} {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/(9-m))}}{{\log (r)}} = \frac{{\log (9-m)}}{{\log (3)}}$$

Examples

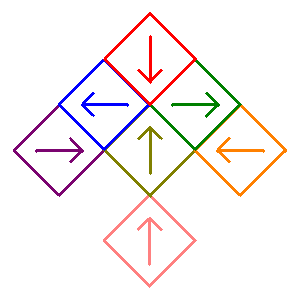
How many examples are possible? There are $\displaystyle \binom{9}{k}$ possible choices for how to remove $k$ squares. Each of the remaining $9-k$ squares can be rotated by one of 4 different angles (0, 90, 180, or 270). Assuming that only between 1 and 7 squares are removed, the total number of possibilities is \[\sum_{k=1}^7 \binom{9}{k}4^{9-k} = 1,690,944.\] However, this counts many designs that are not symmetric with respect to a vertical line through the middle of the initial square. In addition, some designs produce the same fractal and therefore should only be counted once. For example, if only the middle square is removed (square 5 in the illustration above), then the resulting fractal will be the Sierpinski carpet regardless of how the other eight squares are rotated (and there are $4^8$=65536 different ways to rotate those eight squares!). Finally, some of the fractals are just reflections across the horizontal line through the middle of the original square and therefore not really distinct images. For example, the following two fractals are such reflections. On the left, with label 142-214-xx1, squares 7 and 8 were removed at each iteration and five other squares were rotated, while on the right, with label 1xx-412-243, squares 2 and 3 were removed at each iteration and five other squares were rotated. Click on the fractal on the right to see its reflection. We would not want to count these as separate examples.

142-214-xx1 1xx-412-243
$flower fractal$ $reflected flower fractal$

[Another view]
[Another view with squares]
[IFS video demonstration]

Click on "Another view" to see a version of the fractal above that was drawn using the chaos game algorithm to plot over 350,000 points which were colored using the idea of "color stealing" developed by Michael Barnsley (pdf link). The fractal consists of seven self-similar pieces which are easy to spot when each piece is colored differently. Click on "Another view with squares" to see the same image but with the nine squares superimposed on top of the fractal, with each self-similar piece contained entirely within a square. Finally, click on "IFS video demonstration" to see the first five iterations of the IFS construction of the fractal.

IFS Video
Demonstration

Here is an example with label 311-214-xxx where the top three squares are removed and three other squares are rotated as illustrated in the diagram. Click on the fractal for a larger view done in cross stitch.

candelabra design $candelabra fractal$

The following chart shows the total number of distinct symmetric fractals when removing from 1 to 7 squares and using possible rotations at each iteration for a total of 1086 possible fractals [Counting Details].

View
Examples

squares removed	1	2	3	4	5	6	7
number of fractals	257	326	230	162	65	35	11

Special
Properties

Suppose that the area of the initial right square is equal to 1 and that m subsquares are removed at each iteration of the construction. How much of the area of the original square is removed in the limit? At the first iteration, each subsquare that is removed has area 1/9, so the total area removed is m/9. There are (9-m) squares left. Each of these have m subsquares of area $(1/9)^2$ removed. So after two iterations, the total area removed is \[\frac{m}{9}+(9-m)\frac{m}{9^2}.\] Continuing the same way with the additional iterations would produce the geometric series \[\sum_{m=1}^{\infty}(9-m)^{m-1}\frac{m}{9^m} = \frac{\frac{m}{9}}{1-\frac{9-m}{9}} = \frac{\frac{m}{9}}{1-1+\frac{m}{9}}=1.\] All of the area has been removed, just as with the Sierpinski carpet!

The two variations on the Sierpinski carpet that come from dividing the rotated square into nine subsquare pieces and dividing a right isosceles triangle into nine triangular pieces have some similarities in that the right isosceles triangle is half of the rotated square, and pairs of triangular pieces make up a subsquare. So it is not surprising that the family of Sierpinski carpet relatives shares some common fractals with the family that comes from subdividing the right isosceles triangle. Here are two examples.

$xxx-111-234 fractal$    $xxx-111-432 fractal$
xxx-111-234 square design    xxx-111-432 square design
xxx-111-234 triangle design    xxx-111-432 triangle design

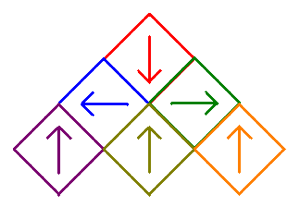
The second row shows the design as Sierpinski carpet relatives xxx-111-234 and xxx-111-432 where the bottom three squares have been removed and squares 7, 8, and 9 have been rotated. The third row shows the design when starting with the isosceles right triangle divided into nine pieces with three being removed. The reason these give the same fractal is that each has an iterated function system with the same scaling and rotation matrices, but just with different translation vectors.

Index	Function	Scaling/Rotation
1.	\({f_1}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {0} \\ {0} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_1\) =

2.	\({f_2}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {-1/6} \\ {1/6} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_2\) =

3.	\({f_3}({\bf{x}}) =\displaystyle \left[ {\begin{array}{c} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {1/6} \\ {1/6} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_3\) =

4.	\({f_4}({\bf{x}}) =\displaystyle \left[ {\begin{array}{*{20}{cc}} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {-1/3} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_4\) =

5.	\({f_5}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {0} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_5\) =

6.	\({f_6}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {1/3} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_6\) =

7.	\({f_7}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {-1/6} \\ {1/2} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_7\) =

8.	\({f_8}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {1/6} \\ {1/2} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_8\) =

9.	\({f_9}({\bf{x}}) =\displaystyle \left[ {\begin{array}{cc} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{c} {0} \\ {2/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by \(\theta_9\) =

Classic Iterated Function Systems