Sierpinski Gasket
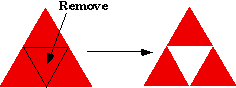
Start with a solid (filled) equilateral triangle \(S_0\). Divide this into four smaller equilateral triangles using the midpoints of the three sides of the original triangle as the new vertices. Remove the interior of the middle triangle (that is, do not remove the boundary) to get \(S_1\). Now repeat this procedure on each of the three remaining solid equilateral triangles to obtain \(S_2\).
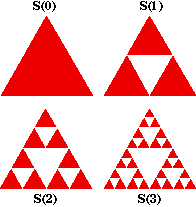
Continue to repeat the construction to obtain a decreasing sequence of sets that converge to a limit [Limit Details].
$$ S_0 \supset S_1 \supset S_2 \supset S_3 \supset \cdots $$
The limit is the Sierpinski gasket, also known as the Sierpinski triangle, and is equal to \(\displaystyle \bigcap_{n=0}^\infty S_n\), the intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often.
Iterated
Function
System
IFS
Animation
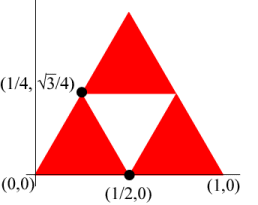
The set \(S_1\) can also be obtained by scaling three copies of \(S_0\) each by a factor of $r$ = 1/2 and then translating two of the smaller triangles to form the desired arrangement. If we imagine the bottom side of \(S_0\) to lie along the x-axis with the vertices at the origin and at the point (1,0), then two of the scaled triangles would have to be translated so that the lower left vertices are at (1/2, 0) and \((1/4, \sqrt 3 /4)\) respectively. This yields the following iterated function system.
IFS
Animation
3 different
initial sets
IFS
Animation
Sierpinski
converges to
his own triangle!
IFS
Animation
Circumscribed
Circles
If you apply the IFS to \(S_1\), you will get \(S_2\). Apply it to \(S_2\) to get \(S_3\), and continue to do this indefinitely. The Sierpinski gasket is the attractor for this IFS. This means that if you apply the iterated function system repeatedly beginning with any initial compact set (such as \(S_0\)), then the resulting images will converge to the Sierpinski gasket, and applying the IFS to the Sierpinski gasket itself will just reproduce the same image. To see some examples of this behavior, view the IFS animation with three different initial sets. You can even make Sierpinski himself converge to his own gasket!
Because of the rotational symmetry of an equilateral triangle, there is second iterated function system that has the Sierpinski gasket as its attractor. In addition to scaling by a factor of $r$=1/2, rotate two of the triangles by 120° and -120°, then translate.
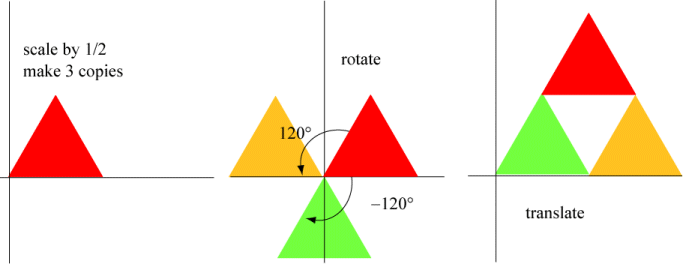
This yields the IFS given by the following three functions.
IFS
Animation
via Line
Segments
If the iterated function system given above is applied to an initial set that is a horizontal line segment, then the first three iterations would be the following:
The construction can also be described this way. Begin with a horizontal line segment. As the first iteration, replace this segment with three segments, each scaled by 1/2, in such a way that the original segment would be the base of a trapezoid with the top parallel to the base. Call this trapezoid (minus the base) the motif. For the second iteration, replace each of the line segments in the first iteration with a copy of the motif scaled by $(1/2)^2$, using the following replacement rules for how to place the copies of the scaled motif relative to the segments in the previous iteration.
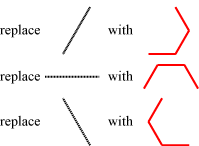
Continue this replacement for each new iteration. At the nth iteration, replace each of the segments of the previous iteration with copies of the motif scaled by a ratio of $(1/2)^n$ using the replacement rules shown above. This construction is referred to as the Sierpinski arrowhead curve. The limit of the iterations as n goes to infinity will be the Sierpinski gasket. Watch the animation to see this convergence.
Zoom
Animation
Tom Edgar's YouTube channel on Mathematical Visual Proofs includes animations of Six Sierpinski Triangle Constructions.
The construction for the Sierpinski gasket can be done with any shaped triangle, not just an equilateral triangle. Try this GeoGebra app to construct a Sierpinski gasket for a triangle of your choice.
L-System
Axiom F
F —> F+F−F−F+F
L-System
Animation ver 1
L-System
Animation ver 2
Suppose we started with just the axiom F, that is, just one side of the triangle. The first iteration generated by the rule given above would be the following
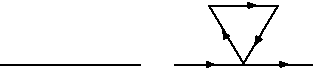
We can see how the rule generates the boundary of the removed inside triangle. Repeated iterations will form more of the interior triangles but will leave out the other two sides of the main triangle. If you watch L-system animation version 1, you will notice that the animation seems to pause occasionally. This is because this L-system will trace some of the sides of the triangles more than once. To see how this happens, watch L-system animation version 2.
L-System
Animation ver 3
Angle 60
Axiom FX
F —> Z
X —> +FY-FX-FY+
Y —> -FX+FY+FX-
This is a bit different in that each curve never intersects with itself as with the first L-system. It corresponds to the Sierpinski arrow curve described above. As such, this construction illustrates that the Sierpinski gasket is actually a plane curve. It corresponds to the construction illustrated above with the second of the iterated function systems when the initial set is a horizontal line.
Below is the fourth iteration of each L-system. Watch the animations for a more detailed view.
Tom Edgar's YouTube channel on Mathematical Visual Proofs includes animations of the 10th iteration of the "Sierpinski Arrowhead Curve L-system".
Similarity
Dimension
The Sierpinski gasket is self-similar with 3 non-overlapping copies of itself, each scaled by the factor $r \lt 1$. Therefore the similarity dimension, $d$, of the attractor of the IFS is the solution to
$$\sum\limits_{k = 1}^3 {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/3)}}{{\log (r)}} = \frac{{\log (1/3)}}{{\log (1/2)}} = \frac{{\log (3)}}{{\log (2)}} = 1.58496$$
Special
Properties
The Sierpinski gasket is also referred to as the Sierpinski triangle or as the Sierpinski triangle curve. It apparently was Mandelbrot who first gave it the name "Sierpinski's gasket." Sierpinski described the construction to give an example of "a curve simultaneously Cantorian and Jordanian, of which every point is a point of ramification." Basically, this means that it is a curve that crosses itself at every point. See the articles [3] and [15] for a good discussion of the origin of the Sierpinski triangle curve.
The following figure shows six Sierpinski gaskets put together in a hexagonal shape. This "curve" also has some interesting topological properties that Sierpinski discussed in his 1915 and 1916 papers. Also see reference [3].
The Sierpinski gasket has area 0. We remove "all" of the area of the initial triangle in constructing the Sierpinski gasket [Area calculations]. But of course there are many points still left in the gasket.
What points are in the Sierpinski gasket? This is an exercise in base-2 (binary) arithmetic. A point $P$ belongs to the Sierpinski gasket if and only if the binary expansions of the barycentric coordinates of $P$, when aligned, have exactly one bit equal to 1 in each position across all three coordinates [Barycentric Details]. There is an alternative characterization for when the initial set is a right triangle rather than an equilateral one! If we take the initial right triangle to have sides of length 1 along the x-axis and y-axis, then the Sierpinski (right) triangle is the set of all pairs \((x,y)\) in the initial triangle that have a binary expansion in which at least one of the corresponding binary digits of \(x\) and \(y\) in each position is 0 [Binomial Details]. You can try both of these yourself using an online Sierpinski Gasket Barycentric Calculator or an online Sierpinski Right Triangle Calculator.
What is the average distance between two points in a unit Sierpinski gasket? The answer is 466 / 885 = 0.52655. Ian Stewart [18] credits this result to Andreas Hinz and describes how the use of graph theory to analyze the n-disk Tower of Hanoi puzzle can be used to calculate this average distance.
Can you beat the computer and win the Sierpinski Gasket "Chaos Game" challenge? The Chaos Game is a well-known method for drawing the Sierpinski Gasket. This challenge features the board shown below that consists of the Sierpinski gasket drawn at a certain level. One of the subtriangles is colored green; this is the Target. You also see a point colored red at one of the numbered corners of the gasket. This is the Seed. Your goal is to move the Seed into the interior of the Target in as few moves as possible.
Can you do it in the minimal number of steps? Click the game board to read the rules and play the game.
Applications? An interesting connection also exists between Pascal's Triangle and the Sierpinski Gasket. There's even some applications to electric circuits!
Artistic Views Could the Sierpinski gasket have captured the imagination of neolithic people in Ireland 5000 years ago? Look at these images and decide for yourself. An article by Elisa Conversano and Laura Tedeschini-Lalli in the 2011 Journal of Applied Mathematics illustrates designs from 11th century Rome churches that are similar to Sierpinski gaskets. Snow artist Simon Beck created a Sierpinski triangle pattern in snow with snowshoes. This was also the February image for the 2013 Calendar of Mathematical Imagery from the American Mathematical Society. Mathematician and artist David A. Reimann created Binomial Pursuit which depicts a Sierpinski triangle where a pursuit triangle is used on the interior triangles, and a simple black outlined triangle is used on the exterior triangles. It was featured as the cover art for the June 2016 issue of Mathematics Magazine.
Variations
The Sierpinski gasket has been constructed using a deterministic method based on subdividing equilateral triangles and removing a central piece. The "chaos game" is an alternative method based on randomness and probability. The chaos game for the Sierpinski gasket is based on repeatedly moving a point half way towards one of three randomly chosen fixed points. We can modify the rules to incorporate rotations of 180° around one or more of the fixed points. Click on the link above for more details and examples of such fractals (such as the ones above).
The Sierpinski gasket can also be constructed by starting with a square that is subdivided into four equal subsquares, then removing the upper right subsquare. By performing one of the 8 symmetry transformations of a square on each of the three remaining subsquares during each step of the iteration, many variations of the Sierpinski gasket can be obtained. Click on the link above for more details and examples of such fractals (such as the one above).
The pedal triangle of an acute triangle $T$ is the triangle formed by the three points that lie at the feet of the three altitudes of $T$, i.e. from each vertex drop a perpendicular to the opposite side until it intersects with that side. The pedal triangle divides the original triangle into four smaller triangles. Remove the interior of the pedal triangle, then repeat the construction on the remaining three triangles.
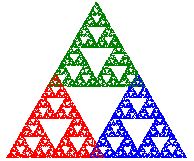
The Sierpinski gasket is formed by scaling an equilateral triangle by the factor $r= 1/2$. Instead of using this scaling factor, however, we can scale the equilateral triangle by a number λ between 0 and 1, make three copies, then translate them to fit back within the original triangle.
Allow the top triangle to rotate around its center. Each rotation produces a different iterated function system with a different attractor. Click on the link above to see an animation of how that changes the Sierpinski gasket.
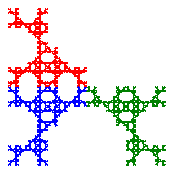
Perform the usual construction for the Sierpinski gasket, but rather than remove the middle triangle, remove the top triangle. The remaining three triangles may be rotated by 120° or 240°, or reflected across one of the altitudes, to form variations on the Sierpinski gasket. Click on the link above for more details and examples of such fractals (such as the one below).
Cascading Sierpinski Triangles
The example of a triangle fractal shown above shows a sequence of Sierpinski triangles shrinking in size. A different version of this is illustrated in the book Brainfilling Curves, by Jeffrey Ventrella. He constructs this as family of non-crossing curves in what he describes as a root4 triangle grid family. It is also the attractor of an IFS with three functions that mimic the usual construction of a Sierpinski triangle. Click on the button to the left for a demonstration.
Curve
Animation
Triangle
Animation
The IFS for this variation employs a reflection across the $x$-axis as well as rotations.
Symmetric Fractal generated from Sierpinski Triangle
Let $S = \{f_1, f_2, f_3\}$ be the three functions in the Sierpinski Triangle IFS. Let $G$ be the cyclic symmetry group $Z_3$. The three elements of $G$ are the identity (no rotation), $r_{120}$, a counterclockwise rotation through 120°, and $r_{240}$, a counterclockwise rotation through 240°. We can form a new IFS by applying each of the symmetries in $G$ to each of the functions in $S$, i.e. form the set of affine transformations $GK = \{ gf : g \in G \text{ and } f \in S\}$. The new IFS would then consist of the 9 functions $\{f_k, r_{120}f_k, r_{240}f_k \text{ for } k = 1,2,3\}$. The first iteration would look like the following (using an equilateral triangle as the initial set as in the construction of the regular Sierpinski triangle).
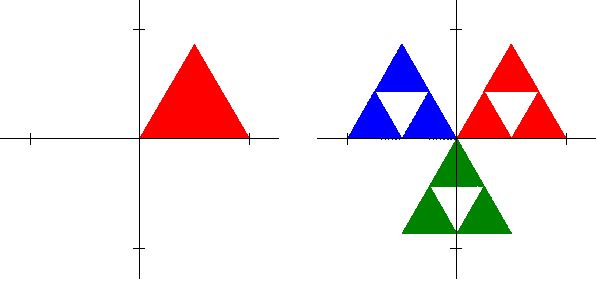
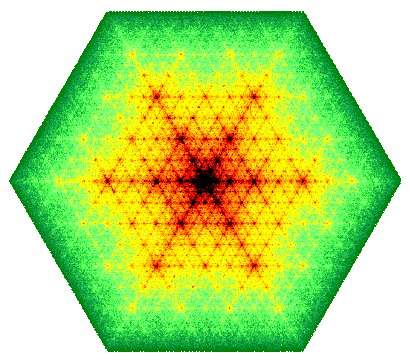
This iterated function system produces the following fractal which actually has six-fold rotational symmetry (in addition to several reflective symmetries). This is because the fixed attractor is a filled-in hexagon [Hexagon Details]. It is colored using pixel counting (the color depends on how many times a particular pixel is plotted during the drawing of the fractal using the random chaos game algorithm). Read more details on symmetric fractals or see the book by Field and Golubitsky.
Sierpinski Valentines
The image on the left is from the webcomic xkcd. The image in the middle was inspired by xkcd and drawn using the software IFS Construction Kit with the heart graphed using the implicit relationship \(x^2+\left(y-\sqrt{|x|}\right)^2 = 2\). Click on the image to the right to view a video version on YouTube made with the ManimCE animation software.
See a similar image implemented in Desmos by Eric Berger.
