

| squares removed | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| number of fractals | 257 | 326 | 230 | 162 | 65 | 35 | 11 |
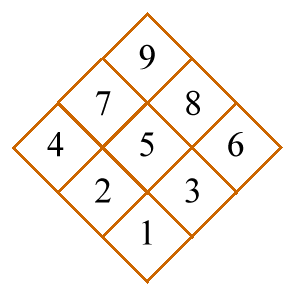
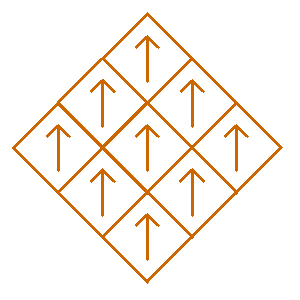
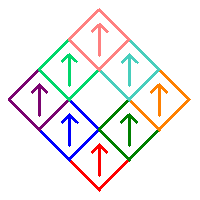
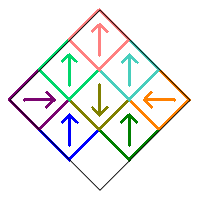
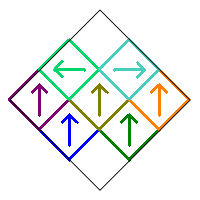
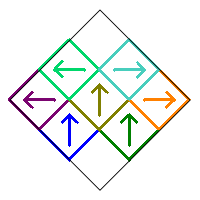
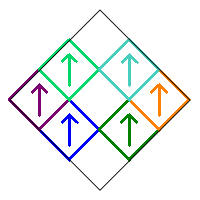
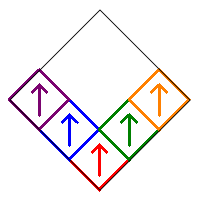
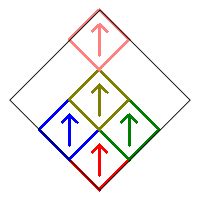
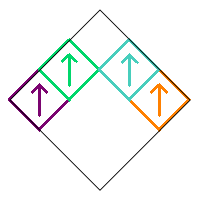
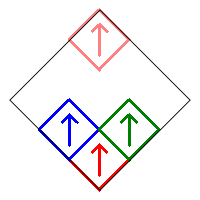
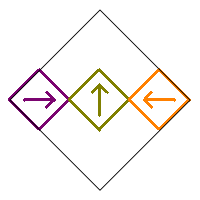
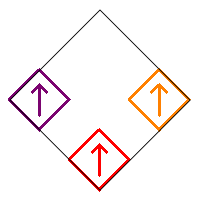
The subsquares are numbered as follows, and initially oriented in the up direction as illustrated by the arrows in the image on the right.
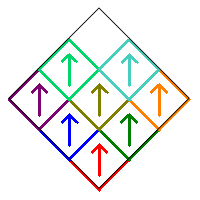
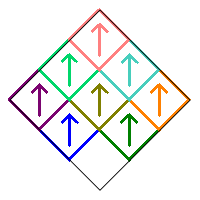
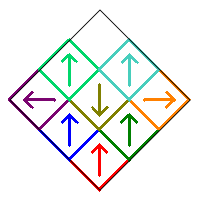
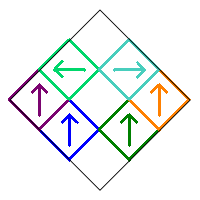
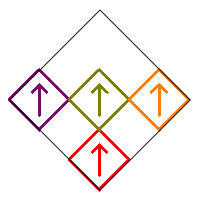
We will restrict our count to Sierpinski Carpet relatives that are symmetric with respect to the vertical diagonal in the initial square. This means that squares 1, 5, and 9 can only be rotated by 0° or 180°. In addition, the squares in the pairs (2,3), (4,6), and (7,8) must either be both pointing up, both pointing down, or one pointing right and the other pointing left. Following is an example of these various symmetric possibilities.
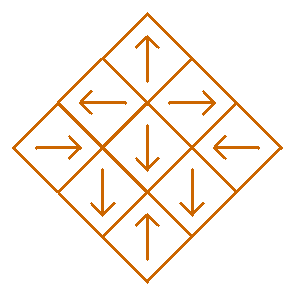
So once a rotation is chosen for squares 2, 4, and 7, the rotations for squares 3, 6, and 8 are uniquely determined. We will also count two fractals as the same if one is a reflection of the other across the horizontal diagonal in the initial square.
Note: All fractals are shown using 4 iterations.
If only 1 square is removed, it must be either square 1, 5, or 9.

Because of the rotational symmetry of the fractal, the image can be rotated 0, 90, 180, or 270 degrees without changing the image. This means that each of the eight remaining squares in the construction can be rotated by any of these angles and the iterative construction will produce the same fractal. So removing square 5 produces only one possible fractal.

Squares 1 and 5 can each be rotated in two ways (0° or 180°), while squares 2, 4, and 7 each have four choices. There are therefore 22×43 = 256 possible choices, and each produces a different fractal.



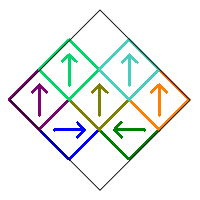
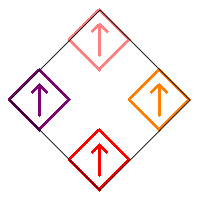
Here is another example where three of the squares (4, 5, and 6) are rotated. Click on either fractal to see its reflected version and notice that both are the same when one is reflected.


This can be done for each of the 256 fractals obtained by removing square 9. Therefore deleting only square 1 does not produce any new fractals, just reflections of the ones from removing only square 9.
The total number of fractals when removing just one square is therefore 1 + 256 + 0 = 257.
There are several cases for how two squares can be removed. As above, certain combinations can produce images that are just reflections of each other. Those will be counted together.
Removing squares 5 and 9 with no additional rotations produces the following fractal on the left. The equivalent reflected version from removing squares 1 and 5 is shown on the right.
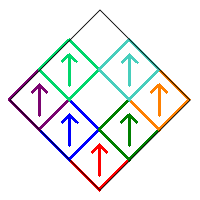

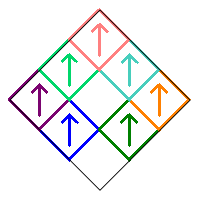

In either case, the remaining square 1 or 9 can be rotated in two ways (0° or 180°), while squares 2, 4, and 7 each have four choices. There are therefore 2×43 = 128 possible choices, and each produces a different fractal.
There are six cases to consider depending on how squares 2, 4, and 7 are rotated.
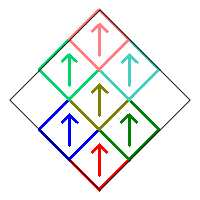
Case 1. Removing squares 1 and 9 with no additional rotations produces the following fractal.
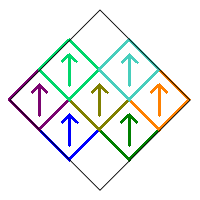

Any of the squares can be rotated by 0° or 180° without changing the fractal because of the 180° rotational symmetry of the image. For example, consider the following design where three of the squares are rotated by 180°.
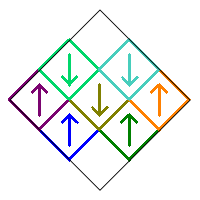

Therefore there is only one possible fractal if all squares are rotated by 0° or 180°.
Case 2. Now consider the fractal when only square 4 is rotated by 90° or 270°. Here square 4 is rotated by 90°, and thus square 6 is rotated by 270°.
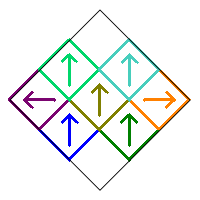

Again, because of the symmetry of the fractal, nothing will change if any of the squares with arrows pointing up are rotated by 180°. In addition, rotating the fractal by either 90° or 270° yields the same design, so it doesn't matter whether square 4 is rotated by 90° or 270°. Therefore there is only one possible fractal when square 4 is rotated.
Case 3. Next consider the fractal when squares 2 and 7 are rotated by 90° or 270°. Here they are both rotated by 90°, and thus squares 3 and 8 are rotated by 270°.
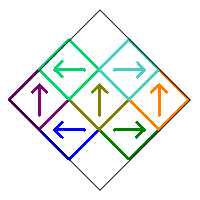

As before, because of the symmetry of the fractal, nothing will change if any of the squares with arrows pointing up are rotated by 180°. In addition, rotating the fractal by either 90° or 270° has the same result, so it doesn't matter whether squares 2 and 7 are rotated by 90° or 270°. Therefore there is only one possible fractal when squares 2 and 7 are rotated.
Case 4: There is one more symmetric case where squares 2, 4, and 7 are rotated by 90° or 270°. Here they are all rotated by 90°, and thus squares 3, 6, and 8 are rotated by 270°.
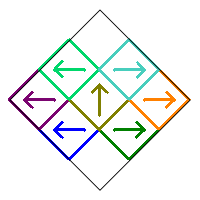

In a similar way as above, because of the symmetry of the fractal this is the only possible image that can occur in this case regardless in how squares 2, 4, and 7 are rotated by either 90° or 270° and square 5 is rotated by 0° or 180°
Case 5. That takes care of all the symmetric cases. Now suppose square 7 is rotated by 90° or 270°. Here is the fractal if square 7 is rotated by 90°, and so square 8 is rotated by 270°.

Because of the lack of symmetry, rotating any of the squares with arrows pointing up by 180° will produce a different fractal, and rotating square 7 by 270° will also produce a different fractal. There are two rotation choices for each of the squares 2, 4, 5, and 7, so the total number of possible fractals in this case is 24 = 16. Each of these 16 fractals has a reflected version obtained by rotating square 2 by 90° or 270° instead of square 7. Here is the reflected companion of the fractal shown above. Click on the fractal to reflect it across the horizontal line.

Case 6. The final case is when squares 4 and 7 are rotated by 90° or 270°. Here is the fractal when both are rotated by 90°.

Because of the lack of symmetry, there are two possible rotation choices for squares 4 and 7, and two possible rotation choices for squares 2 and 5, for a total of 24 = 16 different fractals. Each of these 16 fractals has a reflected version obtained by rotating squares 2 and 4 by 90° or 270° instead of squares 4 and 7.
This exhausts all possible cases when squares 1 and 9 are removed. Adding up the different number of fractals gives 1+1+1+1+16+16 for a total of 36.There are three cases depending on how squares 2 and 7 are rotated.
Case 1. Removing squares 4 and 6 with no additional rotations produces the following fractal.

Because of the symmetry of the fractal, any of the squares can be rotated by 0° or 180° without changing the image. Therefore there is only one possible fractal if all squares are rotated by 0° or 180°.
Case 2. Consider when square 7 is rotated by 90° or 270°. Here square 7 is rotated by 90° (and thus square 8 is rotated by 180°).
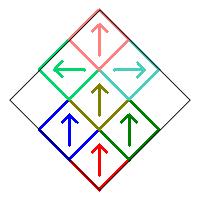

Because of the lack of symmetry, rotating any of the squares with arrows pointing up by 180° will produce a different fractal, and rotating square 7 by 270° will also produce a different fractal. There are two rotation choices for square 7 and also two rotation choices for each of the squares 1, 2, 5, and 9, so the total number of possible fractals in this case is 25 = 32. Each of these 32 fractals has a reflected version obtained by rotating square 2 by 90° or 270° instead of square 7.
Case 3. For the final case, consider when both square 2 and 7 are rotated by 90° or 270°. Here square 7 is rotated by 90° (and thus square 8 is rotated by 270°), and square 2 is rotated by 270° (and thus square 3 is rotated by 90°).
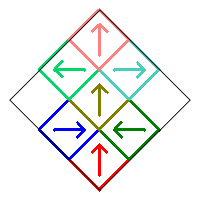

As in other cases above, because of the symmetry of the fractal this is the only possible image that can occur in this case regardless in how squares 2 and 7 are rotated by either 90° or 270° and squares 1, 5, and 9 are rotated by 0° or 180°.
This exhausts all possible cases when squares 1 and 9 are removed. Adding up the different number of fractals gives 1+32+1 for a total of 34.
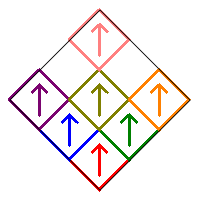

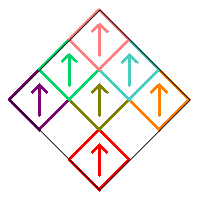

In either case, the remaining squares 1, 5, and 9 can be rotated in two ways (0° or 180°), while squares 2 and 4, or 4 and 7 for the reflected version, each have four choices. There are therefore 23×42 = 128 possible choices, and each produces a different fractal.
The total number of fractals when removing two squares is therefore 128+36+128+34=326.
There are several cases for how three squares can be removed. As above, certain combinations can produce images that are just reflections of each other. Those will be counted together.
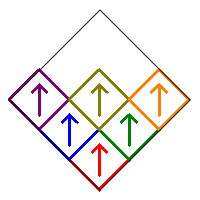
This is very similar to the situation for removing two squares where squares 1 and 9 are removed. So the six cases illustrated above for that situation still apply, but square 5 will no longer be involved. The symmetric cases still give only one fractal, whereas the two non-symmetric designs will now only produce 8 fractals each instead of 16. Therefore there will be a total of 1+1+1+1+8+8=20 difference fractals. Here are two examples.


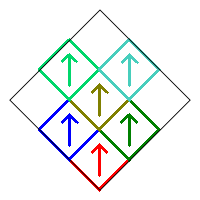
This is very similar to the situation for removing two squares where squares 4 and 6 are removed. So the three cases illustrated above for that situation still apply, but square 5 will no longer be involved. The symmetric cases still give only one fractal, whereas the one nonsymmetric design will now only produce 16 fractals each instead of 32. Therefore there will be a total of 1+16+1=18 difference fractals.
Removing squares 7, 8, and 9 with no additional rotations produces the following fractal.

The remaining squares 1 and 5 can be rotated in two ways (0° or 180°), while squares 2 and 4 each have four choices. There are therefore 22×42 = 64 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 2, and 3.
Removing squares 4, 6, and 9 with no additional rotations produces the following fractal.

The remaining squares 1 and 5 can be rotated in two ways (0° or 180°), while squares 2 and 7 each have four choices. There are therefore 22×42 = 64 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 4, and 6.
Removing squares 2, 3, and 9 with no additional rotations produces the following fractal.
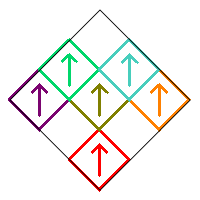

The remaining squares 1 and 5 can be rotated in two ways (0° or 180°), while squares 4 and 7 each have four choices. There are therefore 22×42 = 64 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 7, and 8.
The total number of fractals when removing two squares is therefore 20+18+64+64+64=230.
There are several cases for how four squares can be removed. As above, certain combinations can produce images that are just reflections of each other. Those will be counted together.
Removing squares 2, 3, 7, and 8 with no additional rotations produces the box fractal rotated by 45°.
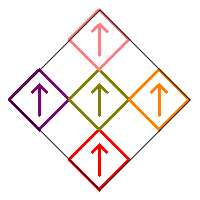

Because of the rotational symmetry of the fractal, the image can be rotated 0, 90, 180, or 270 degrees without changing the image. This means that each of the five remaining squares in the construction can be rotated by any of these angles and the iterative construction will produce the same fractal. So removing these four squares produces only one possible fractal.
Removing squares 1, 4, 6, and 9 with no additional rotations produces the following image.
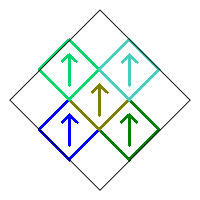

Because of the rotational symmetry of the fractal, the image can be rotated 0, 90, 180, or 270 degrees without changing the image. This means that each of the five remaining squares in the construction can be rotated by any of these angles and the iterative construction will produce the same fractal. So removing these four squares produces only one possible fractal.
Removing squares 4, 5, 6, and 9 with no additional rotations produces the following fractal.
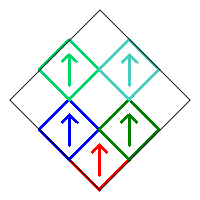

The remaining square 1 can be rotated in two ways (0° or 180°), while squares 4 and 7 each have four choices. There are therefore 2×42 = 32 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 4, 5, and 6.
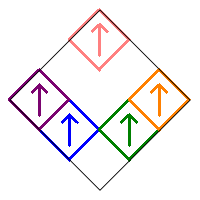
Removing squares 5, 7, 8, and 9 with no additional rotations produces the following fractal.

The remaining square 1 can be rotated in two ways (0° or 180°), while squares 2 and 4 each have four choices. There are therefore 2×42 = 32 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 2, 3, and 5.
Removing squares 1, 5, 7, and 8 with no additional rotations produces the following fractal.
The remaining square 9 can be rotated in two ways (0° or 180°), while squares 2 and 4 each have four choices. There are therefore 2×42 = 32 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 2, 3, 5, and 9.
Removing squares 1, 7, 8, and 9 with no additional rotations produces the following fractal.
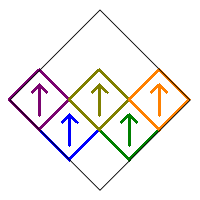

The remaining square 5 can be rotated in two ways (0° or 180°), while squares 2 and 4 each have four choices. There are therefore 2×42 = 32 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 2, 3, and 9.
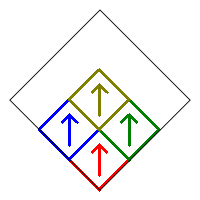
Removing squares 4, 6, 7, and 8 with no additional rotations produces the following fractal.

The remaining squares 1, 5, and 9 can be rotated in two ways (0° or 180°), while square 2 has four choices. There are therefore 4×23 = 32 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 2, 3, 4, and 6.
The total number of fractals when removing four squares is therefore 1+1+32+32+32+32+32=162.
There are several cases for how five squares can be removed. As above, certain combinations can produce images that are just reflections of each other. Those will be counted together.
Removing squares 2, 3, 5, 7, and 8 with no additional rotations produces the following fractal.
Because of the rotational symmetry of the fractal, the image can be rotated 0, 90, 180, or 270 degrees without changing the image. This means that each of the five remaining squares in the construction can be rotated by any of these angles and the iterative construction will produce the same fractal. So removing these four squares produces only one possible fractal.
Removing squares 4, 6, 7, 8, and 9 with no additional rotations produces the following fractal.
The remaining squares 1 and 5 can be rotated in two ways and square 2 can be rotated in four ways. There are therefore 4×22 = 16 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 2, 3, 4, and 6.
Removing squares 1, 5, 7, 8, and 9 with no additional rotations produces the following fractal.
The remaining squares 2 and 4 can be rotated in four ways. There are therefore 42 = 16 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 2, 3, 5, and 9.
Removing squares 2, 3, 7, 8, and 9 with no additional rotations produces the following fractal.

The remaining squares 1 and 5 can be rotated in two ways (0° or 180°), while square 4 has four choices. There are therefore 4×22 = 16 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 1, 2, 3, 7, and 8.
Removing squares 4, 5, 6, 7, and 8 with no additional rotations produces the following fractal.
The remaining squares 1 and 9 can be rotated in two ways (0° or 180°), while square 2 has four choices. There are therefore 4×22 = 16 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing squares 2, 3, 4, 5, and 6.
The total number of fractals when removing five squares is therefore 1+16+16+16+16=65.
There are several cases for how six squares can be removed. As above, certain combinations can produce images that are just reflections of each other. Those will be counted together.
Removing all squares except for squares 1, 5, and 9 without rotating any of the remaining squares produces the following image (just a vertical line segment, so technically not really a fractal).
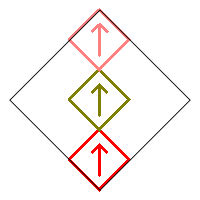

Any of the remaining three squares can be rotated by 180° without changing the final image, so there is only one possibility in this case.
Removing all squares except for squares 4, 5, and 6 without rotating any of the remaining squares produces the following image (just a horizontal line segment, so technically not really a fractal).
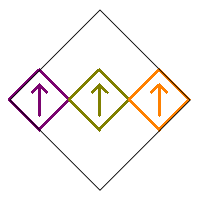
The image will not change if any of the squares are rotated by 180° If square 4 is rotated by 270° (and thus square 6 by 90°), the result is shown below.
The same fractal would result whether square 5 is pointing up or down, and whether square 4 is pointing left or right. Therefore these two images are the only possibilities when all squares except 4, 5, and 6 are removed.
Removing all squares except for squares 1, 2, and 3 without rotating any of the remaining squares produces the following fractal.
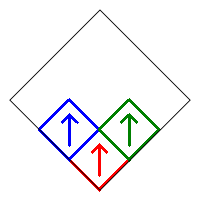
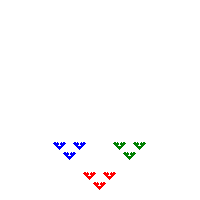
The remaining square 1 can be rotated in two ways (0° or 180°), while square 2 has four choices. There are therefore 4×2 = 8 possible choices, and each produces a different fractal. Each of these has a corresponding reflected version obtained by removing all squares except 7, 8, and 9.
The following three cases are similar to the one above, and each has 8 possible choices.

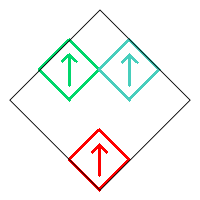

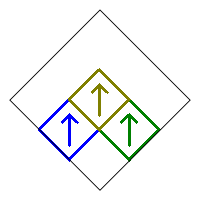

The total number of fractals when removing five squares is therefore 1+2+8+8+8+8=35.
Following are the four basic designs from removing 7 squares and not rotating the remaining two.
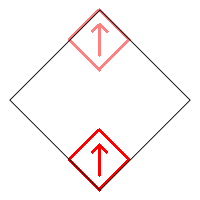
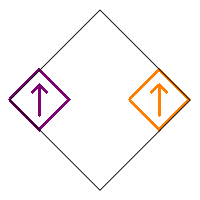
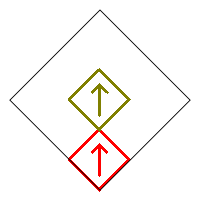
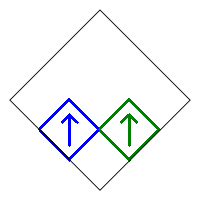
The first produces a vertical Cantor set. The second produces a horizontal Cantor set. The other two produce Cantor like sets. Including rotations, there are a total of 1+2+4+4=11 different possible fractals from the four designs (and their reflective companions).
See a Gallery of some of the Sierpinski Carpet relatives.
See some video demonstrations of the IFS construction of some of the Sierpinski Carpet relatives.