
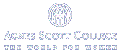

IFS Construction Kit can be used to design and draw fractals based on iterated function systems. The program consists of three main windows. The IFS Window is where you can see and edit the code for the transformations that comprise the IFS. This window also shows the scale used in the other two windows. The Design window shows the effects of the transformations on an initial polygon. You can translate, scale, rotate, stretch, or shear transformations using the mouse, keyboard, or through a dialog box. This provides a way to define or modify transformations without having to enter the numbers in the IFS window. If you display the Preview window (from the Design menu), you can get immediate feedback on how the fractal changes as you modify the transformation. The Fractal window is where you draw the fractal obtained by iterating the transformations in the IFS, either by using the Random Algorithm or the Deterministic Algorithm.
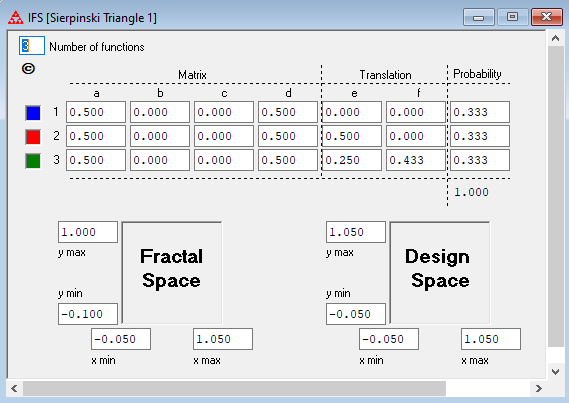
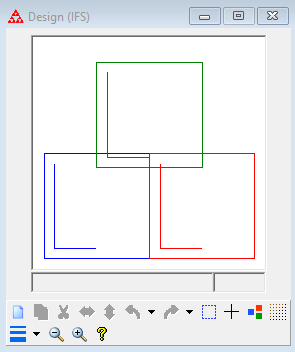
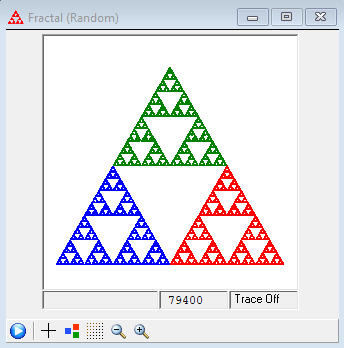
The software can be downloaded at https://larryriddle.agnesscott.org/ifskit/index.htm.
This is a python program to use turtle graphics to draw the fractals of iterated function systems described by an L-system. It should work on Macs, Windows, or Linux systems that have python 3 installed. The input provided to the program is:
Input can be entered manually or via a text file in the same directory as the program. The graphic window size (7) and number of iterations (8) are not part of the file and will always be entered manually while program is running. After the fractal is drawn for a specified iteration, the program will ask for another iteration value until the user enters 0 (or any negative value).
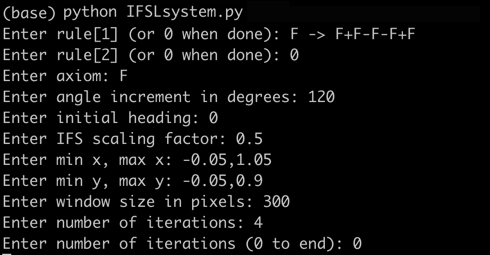
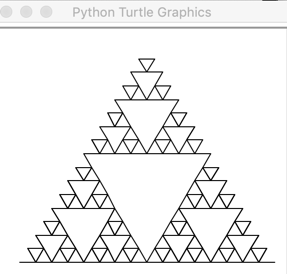
The program and IFS example files can be downloaded at https://github.com/mathriddle/IFS-Lsystem.
An alternative to running IFSLsystem.py in a terminal window on a Mac, Windows, or Linux computer is to run it in a Colaboratory or Jupyterlab notebook in a web browser. This requires using the ColabTurtlePlus package available at PyPI to handle the turtle graphics in the web browser. This package is an extension of the original ColabTurtle by Tolga Atam. One of the advantages of this approach is that the fractal image can be saved as a SVG file. See the PyPI Readme file or the documentation for more information about ColabTurtlePlus and how to use it in Colab or Jupyterlab. The Github repository is https://github.com/mathriddle/ColabTurtlePlus
Here is an SVG image of the 3rd iteration of the Sierpinksi triangle from an L-system that was drawn using the Colab notebook IFSTurtleGraphics.ipynb which can be opened in Google Colab (if you have a Google account). Or you can download a Jupyter notebook.
The animated video demonstrations about Sierpinski Relatives construction, tiling, and friezes were created using Manim Community Edition, a community maintained Python library for creating mathematical animations. Manim stands for mathematical animation engine and was created by Grant Sanderson of 3Blue1Brown YouTube fame to produce math animation videos. I created my animations by installing Manim in a Google Colaboratory environment.