Right Triangle Divided by Nine

The construction of these fractals is motivated by the web page "Right triangle divided by nine" by Robert Fathauer, part of his website on Gasket Fractals. Start with a right isosceles triangle. Divide that triangle into nine similar right triangles as shown in the following figure.

Remove one or more of the smaller triangles, then iterate the construction on the remaining right triangles. The following sequences of images shows the first four iterations if only the top triangle is removed during each iteration.

In the two figures below, two triangles have been removed. Click on the images to see the resulting gasket fractal.

   

In the next two figures, three triangles have been removed. Click on the images to see the resulting gasket fractal.

   

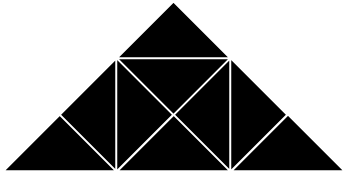
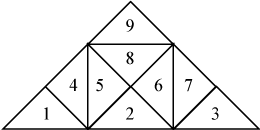If the nine triangles are labeled from 1 to 9 as shown to the right, then each of the functions corresponding to a particular triangle can be indexed by the same number as the triangle. This gives the following nine functions.
 

\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {0} \\ {0} \\ \end{array}} \right]\)	scale by 1/3
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {2/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {0} & {-1/3} \\ {1/3} & {0} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3, rotate by 90°
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {0} & {1/3} \\ {-1/3} & {0} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by –90°
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {0} & {-1/3} \\ {1/3} & {0} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {2/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3, rotate by 90°
\({f_7}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {0} & {1/3} \\ {-1/3} & {0} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {2/3} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by –90°
\({f_8}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {-1/3} & {0} \\ {0} & {-1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {2/3} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by 180°
\({f_9}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/3} & {0} \\ {0} & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {1/3} \\ \end{array}} \right]\)	scale by 1/3

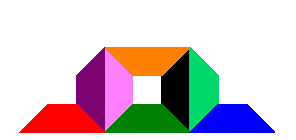
After deciding which triangles will be removed to construct the fractal, the IFS for that fractal will consist of the functions above whose indices match those of the remaining triangles. For example, if the lower left and lower right triangles are removed (triangles 1 and 3) as shown above, then the IFS for the resulting fractal is the set \(\{f_2,f_4,f_5,f_6,f_7,f_8,f_9\}\).

Suppose \(m\) triangles are removed at each iteration of the construction, where \(1 \le m \le 7\) (if you remove 8 triangles, leaving only one, the limit of the iteration will be a single point.) The resulting fractal is self-similar with \((9-m)\) non-overlapping copies of itself, each scaled by the factor r = 1/3. Therefore the similarity dimension, d, of the attractor of the IFS is the solution to

$$\sum\limits_{k = 1}^{9-m} {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/(9-m))}}{{\log (r)}} = \frac{{\log (9-m)}}{{\log (3)}}$$

m	Pattern	Gasket	Similarity Dimension
1		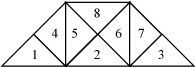	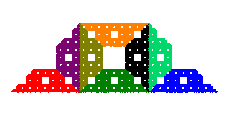1.89279
2		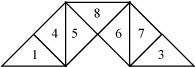	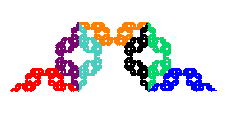1.77124
3		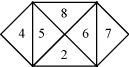	1.63093
4		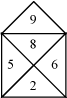	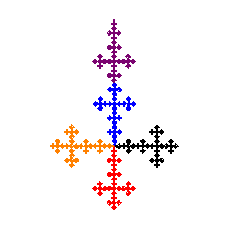1.46497
5		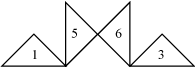	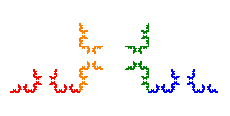1.26186
6		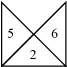	1.0
7		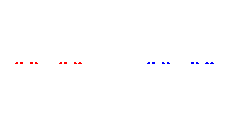	0.63093

In these examples, the last one (m = 7) is the Cantor ternary set built by removing the middle third of a line segment and iterating the process on the two remaining segments. Another example for m = 6 is to remove all but the bottom three triangles (leaving triangles 1, 2, and 3). The fixed attractor for this IFS would just be a line segment, so its similarity dimension of 1 would be the same as its topological dimension. The line segment would not be considered a fractal.

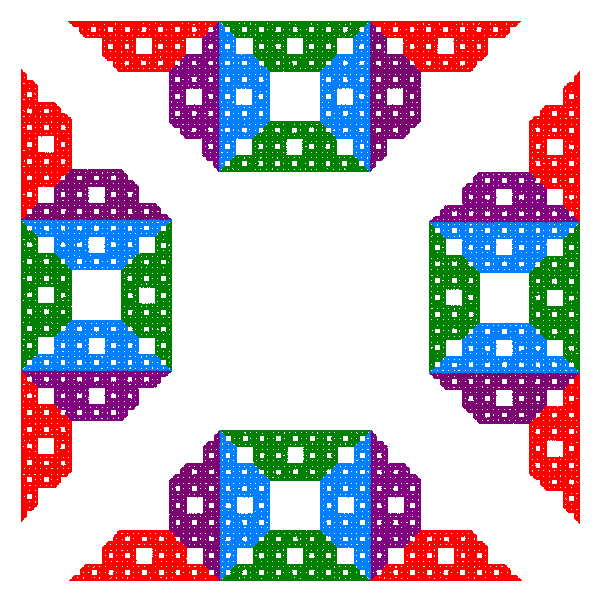
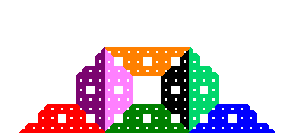
The following cross-stitch design shows the four examples depicted in the Description section above. Click on the image for an enlarged view.

Larry Riddle, 2019
(5 iterations on 28 count per inch fabric, 16" x 20")

How many examples are possible? There are \(\displaystyle \binom{9}{k}\) possible choices for how to remove \(k\) triangles. Assuming that only between 1 and 7 triangle are removed, the total number of possibilities is \[\sum_{k=1}^7 \binom{9}{k} = 501.\] However, some of the resulting fractals are just reflections across the vertical line through the middle of the original triangle and therefore not really distinct images. For example, the following two fractals are such reflections. On the left, only the lower left triangle (triangle 1) was removed at each iteration, while on the right, only the lower right triangle (triangle 3) was removed at each iteration. We would not want to count these as separate examples.

  

Similarly, the fractals obtained by removing triangle 4 and triangle 7, respectively, are mirror images, as are the two fractals obtained by removing triangles 5 and 6, respectively. Thus there are only 6 distinct fractals formed by removing 1 triangle. The following chart shows the total number of distinct fractals when removing from 1 to 7 triangles at each iteration for a total of 280 possible fractals [Details].

triangles removed	1	2	3	4	5	6	7
number of fractals	6	21	47	69	69	47	21

 

Suppose that the area of the initial right triangle is equal to 1 and that m triangles are removed at each iteration of the construction. How much of the area of the original triangle is removed in the limit? At the first iteration, each triangle that is removed has area 1/9, so the total area removed is m/9. There are (9-m) triangles left. Each of these have m triangles of area (1/9)² removed. So after two iterations, the total area removed is \[\frac{m}{9}+(9-m)\frac{m}{9^2}.\] Continuing the same way with the additional iterations would produce the geometric series \[\sum_{m=1}^{\infty}(9-m)^{m-1}\frac{m}{9^m} = \frac{\frac{m}{9}}{1-\frac{9-m}{9}} = \frac{\frac{m}{9}}{1-1+\frac{m}{9}}=1.\] All of the area has been removed, just as with the Sierpinski carpet!

Four copies of the gasket generated by removing only the top triangle can be combined to give the Sierpinski carpet as illustrated below.

1. For other examples of similar gasket fractals, see Robert Fathauer's website at https://mathartfun.com/fractaldiversions/GasketHome.html.