$$ C(0) \supset C(1) \supset C(2) \supset C(3) \supset \cdots $$
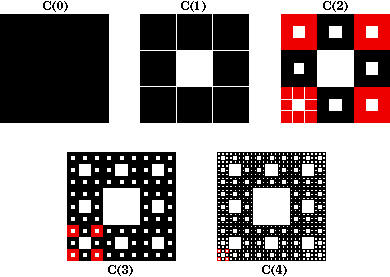
The Sierpinski carpet is the intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often. The figures below show the first four iterations. The squares in red denote some of the smaller congruent squares used in the construction.
Sierpinski
Converges
to his
Carpet
\[ \begin{align} f_1 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} \\ f_2 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} 0 \\ {1/3} \\ \end{array}} \right] \\ f_3 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} 0 \\ {2/3} \\ \end{array}} \right] \\ f_4 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {1/3} \\ 0 \\ \end{array}} \right] \\ f_5 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {1/3} \\ {2/3} \\ \end{array}} \right] \\ f_6 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {2/3} \\ {0} \\ \end{array}} \right] \\ f_7 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {2/3} \\ {1/3} \\ \end{array}} \right] \\ f_8 ({\bf{x}}) &= \left[ {\begin{array}{*{20}c} {1/3} & 0 \\ 0 & {1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}c} {2/3} \\ {2/3} \\ \end{array}} \right] \\ \end{align} \]
The Sierpinski carpet consists of eight self-similar pieces corresponding to the eight functions in the iterated function system.
This will produce the Sierpinski carpet rotated by 45°. In addition, there will be lines through the square "holes" (see first animation). If you want to avoid those lines, you can modify the L-system to lift the pen by using
F —> F+F−F−F−UGD+F+F+F−F
where U means the pen goes up and D means the pen goes down. You can see the effect in the second animation.
$$\sum\limits_{k = 1}^8 {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/8)}}{{\log (r)}} = \frac{{\log (1/8)}}{{\log (1/3)}} = \frac{{\log (8)}}{{\log (3)}} = 1.89279$$
Another way to compute the area of the Sierpinski carpet is to compute the area of the "holes" using self-similarity. Suppose that the square covering the carpet has area 1 (as we did with C(0) above.) Let \(A\) be the area of the "holes" in the carpet. Then \(A = \frac{1}{9}+8\left(\frac{1}{9}A\right)\), the area of the center "hole" plus the areas of the holes in the eight copies of the carpet surrounding the center "hole", each of which is a 1/3-scaled version of the carpet so the area of those "holes" is scaled by 1/9. Then $$A = \frac{1}{9}+\frac{8}{9}A \Rightarrow \frac{1}{9}A = \frac{1}{9} \Rightarrow A = 1.$$ Thus the "holes" have the same area as the covering square, whence Sierpinski's carpet has area 0.
This means that we have removed "all" of the area of the original square in constructing the Sierpinski carpet. But of course there are many points still left in the carpet. That is one reason why area is not a useful dimension for this set.
Sierpinski used the carpet to catalogue all compact one-dimensional objects in the plane (from a topological point of view). What this basically means is the Sierpinski carpet contains a topologically equivalent copy of any compact one-dimensional object in the plane. Thus for any curve contained in the plane, there is a set homeomorphic to the Sierpinski carpet that contains the curve. For a good discussion of this idea, consult the text by Peitgen, Jurgens, and Saupe [6], or the topology text by Engelking and Sieklucki [2].
In an article written in 1916, Sierpinski wrote [1]:
Note that as early as one year ago Mr. Mazurkiewicz found an example of a curve which was simultaneously a Jordan curve and a Cantor curve...Mazurkiewicz forms this curve by dividing the square into nine smaller squares using lines parallel to the sides and removing the interior of the center square, performing the same procedure on each of the remaining eight square, and iterating this procedure ad infinitum.So the Sierpinski carpet was actually invented by Stefan Mazurkiewicz, who in 1913 wrote his Ph.D. thesis under the supervision of Sierpinski on curves filling a square.
Rather than remove the center square at each stop of the iterative construction, keep the center square and the four corner squares but remove the other four middle squares along each edge. The produces the box fractal.
The Sierpinski carpet could be thought of as gasket formed from a "square box divided by nine". Instead of a square, start with a right triangle and divide that right triangle into nine similar right triangles. Remove from 1 to 7 of the smaller triangles, then iterate. This produces what Robert Fathauer has called the "Right Triangle Divided by Nine" gasket.
For other examples of how the Sierpinski Carpet has been an artistic inspiration, see the pictures of the quilt "Sierpinski Meets Mondrian" designed by Professor Gerda de Vries, University of Alberta; or the quilt "An Infinity of Nine-Patches" by Anabeth Dollins, Penn State University Greater Allegheny Campus; or the Sierpinski Carpet in interlocking crochet by Kate Dudman on Instagram.
During October and November 2014, twenty primary sites around the world participated in the MegaMenger challenge. As a distributed fractal project, twenty Menger Sponge cubes were built in different cities around the world. In each location, volunteers built 8,000 small cubes out of nearly 50,000 business cards. These were then combined in groups of 20 to create 400 level one Menger Sponges. These were also combined in groups of 20 to make 20 level two sponges, which then formed one massive level three Menger Sponge. The resulting fractal cube would be nearly 5 feet tall. Collectively, these twenty level three sponges could be virtually combined to form a level-4 Menger sponge, perhaps the largest fractal ever built. Here are pictures of the level three Menger sponge built by faculty and students at Agnes Scott College under the guidance of Assistant Professor of Mathematics, Rachel Bayless (with additional contributions from students at several local middle and high schools).
