


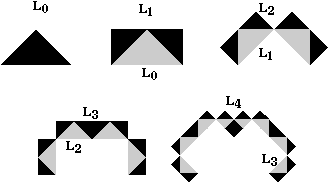
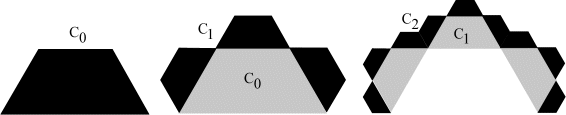
For each new iteration, replace each triangle in Lk by two isosceles right triangles. The Lévy dragon is the limiting set of this iterative construction. Notice that at each iteration, the sides of each triangle in Lk are scaled by a factor \({\bf{r}} = \frac{1}{{\sqrt 2 }}\) [see IFS discussion below], so that the area is scaled by 1/2. But each triangle in Lk produces two new triangles, so the total area remains unchanged. Thus the area of the Lévy dragon is the same as the area of the original isosceles right triangle L0.
Construction
Animation
Geogebra
Animation
Begin with a horizontal line segment. Specify the left endpoint as the "initial" point. As the first iteration, replace this segment with two segments at right angles, each scaled by a ratio \({\bf{r}} = \frac{1}{{\sqrt 2 }}\). Following the orientation along the original segment starting at the initial point, we place the two new segments to the left. For the second iteration, replace each of the segments with two new segments at right angles, each scaled by the ratio r. The new segments are again placed to the left moving along the segments of the first iteration from the initial point. Continue this construction, always placing the new segments to the left along the segments of the previous iteration. The line segments correspond to the hypotenuses of the isosceles right triangles generated in the construction described above. This generates the "dragon curve". The following figure shows the first three iterations for this construction.

Each iteration can be represented symbolically by a sequence consisting of the letters R L, S, and B. One can imagine moving along the individual segments making up the curve starting at the left endpoint. A corner is labeled R if the curve makes a right turn there of 90°, is labeled L if the curve makes a left turn of 90° at that corner, is labeled S if the curve continues straight at that corner (0° turn), and is labeled B if the curve make a 180° turn at that corner. So the three iterations shown above are represented by the sequences R, RSR, and RSRLRSR, respectively. [Details]
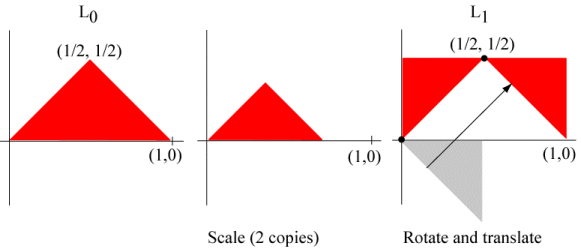
One triangle must then be rotated by 45°, while the other triangle must be rotated by -45° (i.e. in the clockwise direction) and translated by 1/2 in both the x and y directions. This yields the following IFS
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0.5} & { - 0.5} \\
{0.5} & {0.5} \\
\end{array}} \right]{\bf{x}}\) |
scale by r, rotate by 45° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 0.5} & { 0.5} \\
{- 0.5} & { 0.5} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
0.5 \\
0.5 \\
\end{array}} \right]\) |
scale by r, rotate by −45° |
where \({\bf{r}} = \frac{1}{{\sqrt 2 }}\) . The attractor of this IFS will be the Lévy dragon. The Lévy dragon consists of two self-similar pieces corresponding to the two functions in the iterated function system.
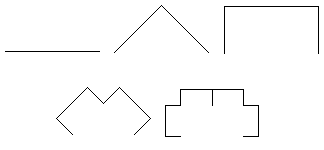
First four iterations of the L-system
The line segments generated by the L-system correspond to the hypotenuses of the isosceles right triangles generated in the construction described above.
\[\sum\limits_{k = 1}^2 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/2)}}{{\log (1/\sqrt 2 )}} = 2\]
Among several of the properties that Lévy observed was that the plane can be tiled by copies of the Lévy dragon. This means that there is a sequence of sets congruent to the Lévy dragon that are non-overlapping and whose unions is the entire plane. Click for more details.
Another property shown by Lévy is that the dragon has non-empty interior [see Edgar]. The paper by Duvall and Keesling investigates some properties of this interior. In addition, the authors develop a theoretical approach to computing the Hausdorff dimension of the topological boundary of attractors of iterated function systems, and apply this theory to estimate that the boundary of the Lévy dragon has Hausdorff dimension of approximately 1.934007183. Bailey, Kim, and Strichartz show that the interior of the Lévy dragon consists of a countable number of components, the largest of which is a hexagon that is only a speck on the dragon. Moreover, they found 16 different shapes for these components and conjectured that there were no others. Alster proved that the number of shapes is finite.
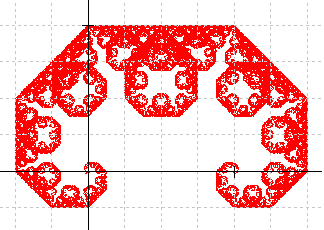
The copy of the Lévy dragon below lies on top of a grid of size 1/4 by 1/4 with the initial line segment going from the origin to the point (1,0). It demonstrates that the Lévy dragon lies within a rectangle with –1/2 ≤ x ≤ 3/2 and –1/4 ≤ y ≤ 1, i.e. a rectangle of width 2 and height 1.25 [Details].
The construction of the Lévy dragon and the Heighway dragon are very similar. In each case one can start with an isosceles right triangle and replace this triangle with two isosceles right triangles so that the hypotenuse of each new triangle lies on one of the equal sides of the old triangle. The difference is how those new triangles are placed relative to sides of the old triangle. For the Lévy dragon, both are placed towards the "outside"; for the Heighway dragon, one is placed pointing out while the other is placed pointing in. Because of this similarity, it is perhaps not surprising that one can transform the Lévy dragon into the Heighway dragon through a continuous transformation. Indeed, for each t in the interval [0,1] define an iterated function system by
|
Inside |
Outside |
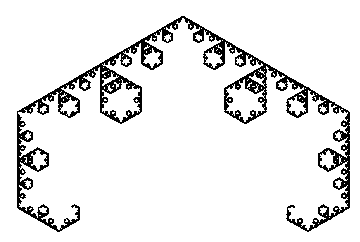
Repeating this construction ad infinitum yields the following figure that looks like it is formed of many diamond shapes of smaller and smaller scale.

Larry Riddle, January 2009
10" x 8" (16 point canvas)
Click on picture for a larger view
[Cross-stitch design (pdf) created with IFS Construction Kit]

Larry Riddle, August 2020
11" x 14" (18 point canvas)
Click on picture for a larger view
The Lévy Tapestry Inside (12 iterations) in back stitch

Larry Riddle, January 2013
12.5" x 12.5" (10 point canvas)
Click on picture for a larger view
[Back stitch design (pdf) created with IFS Construction Kit]
The Lévy Tapestry Outside (12 iterations) in back stitch

Larry Riddle, April 2013
12.5" x 12.5" (18 point canvas)
Click on picture for a larger view
[Back stitch design (pdf) created with IFS Construction Kit]