
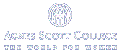


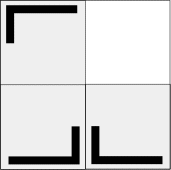
As a variation, however, we can rotate or reflect the scaled squares, thereby changing the orientation. For example, suppose we rotate the upper left square by 90° counterclockwise. This would have the following pattern.
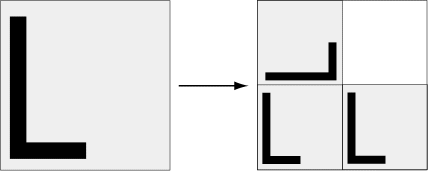
Repeat these steps ad infinitum, always taking into account the current orientation. This yields the following fractal image.
The IFS for this fractal is given by the following three functions corresponding to the three squares from top left to bottom right.
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{0} & {-1/2} \\
{1/2} & {0} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/2} \\
{1/2} \\
\end{array}} \right]\) |
scale by 1/2, rotate by 90° |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & 0 \\
0 & {1/2} \\
\end{array}} \right]{\bf{x}}\) |
scale by 1/2 |
| \({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & 0 \\ 0 & {1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/2} \\ 0 \\ \end{array}} \right]\) | scale by 1/2 |

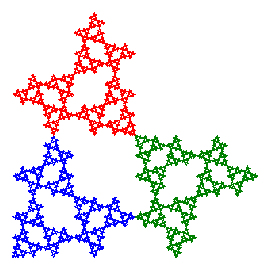
Each transformation has been labeled by a number from 1 to 8. We can apply any of these transformations to the squares in the construction above and the three remaining squares will still fit together as before. Only the orientation of each square may be different. Repeating the construction recursively on the remaining three squares will produce a fractal that is a relative of the Sierpinski gasket. We can identify each pattern in the design for the fractal by the three digits associated with the transformations applied to the three squares, with the digits read from the top left to the lower right. So the construction shown above would be labeled as 211 since the transformation used for the upper left square is a rotation by 90° (transformation 2) while no change is made to the other two squares. Click here for details on the dihedral group of order 8 and formulas for the iterated function systems.
 214 |
 |
|||
 316 |
 |
|||
 184 |
 |
|||
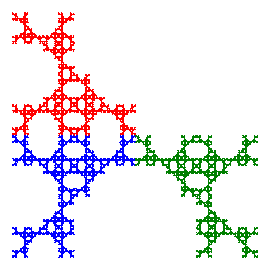
 748 |
 |
|||
 432 |
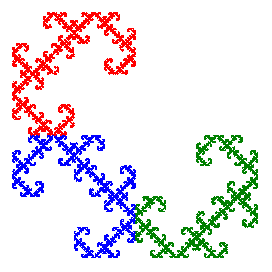 |
|||
 427 |
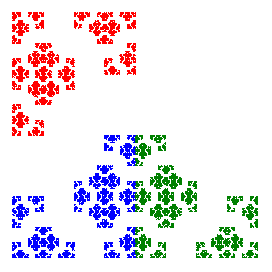 |
In these examples, the last one is totally disconnected, the penultimate one is simply connected (no holes), and the first four are connected, but not simply connected, with infinitely many holes just as with the Sierpinski gasket. There is also a fourth type that has infinitely many connected components, such as the fractal 211 shown above. See the papers by T.D. Taylor for more details about the connectivity properties of Sierpinski relatives.
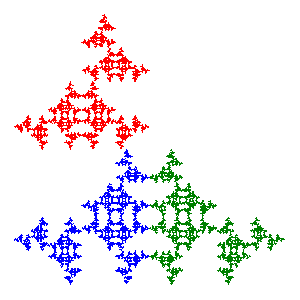
Each Sierpinski relative can be described by a sequence of three digits corresponding to the transformations applied to each of the three squares in the pattern for that fractal. Because there are 8 possible transformations, there are 8x8x8 = 512 possible sequences. But different sequences might produce the same fractal. Notice that example 1 (214) and example 5 (432) above are both symmetric (with respect to a diagonal reflection). There are 8 such symmetric fractals as shown below in two counted cross-stitch designs. The four on the left all have 1 as the middle digit in the sequence corresponding to the transformations [see construction videos], while the four on the right all have 3 as the middle digit [see construction videos].


Larry Riddle, 2009/2010
Sierpinski Theme and Variations
(7 iterations on 25 count per inch fabric, 12.5" x 12.5")
Click on each picture for a larger view.
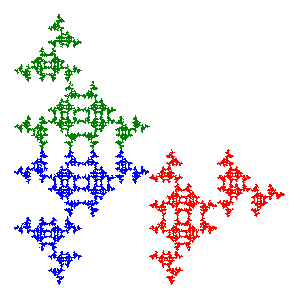
Each of these 8 symmetric fractals can be formed from 8 different sequences of the transformations on the square. This accounts for a total of 64 sequences. The remaining 448 sequences produce fractals that are non-symmetric. They come in pairs, however, with the corresponding fractals symmetric to each other with respect to a reflection across the diagonal. For example, the picture below shows the fractals for the pair (627) and (745). Since these symmetric pairs are essentially the same fractal, the total number of fractals is 8 + 224, or 232. [Counting Details].
$$\sum\limits_{k = 1}^3 {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/3)}}{{\log (r)}} = \frac{{\log (1/3)}}{{\log (1/2)}} = \frac{{\log (3)}}{{\log (2)}} = 1.58496$$
Taylor and Rowley have investigated the convex hulls of the Sierpinski relative fractals. While these convex hulls can be quite complicated, for the eight symmetric relatives they are simple polygonal figures with at most 8 sides. Consequently, it is possible to form tiles and friezes by combining copies of the convex hull of a particular symmetric Sierpinski relative. For more details and some examples, see Tiling Sierpinski Relative Fractals.