


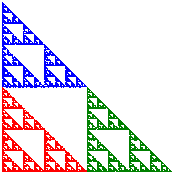
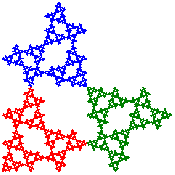
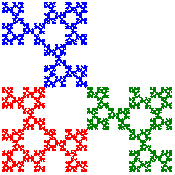


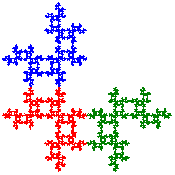

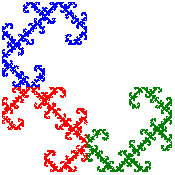
[Alternative View]
[Cross Stitch Design]
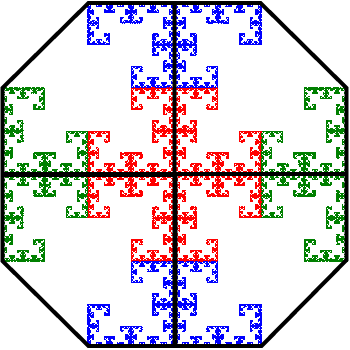
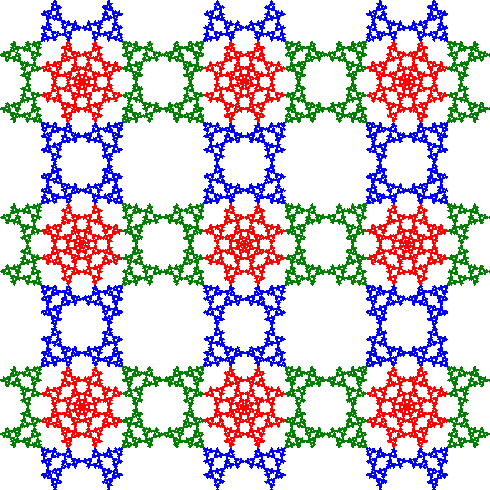
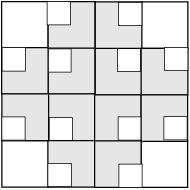
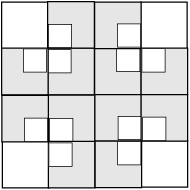
This tile can now be repeated in both the horizontal and vertical directions as shown below. Click on the image to toggle between the image with and without the tile boundaries.
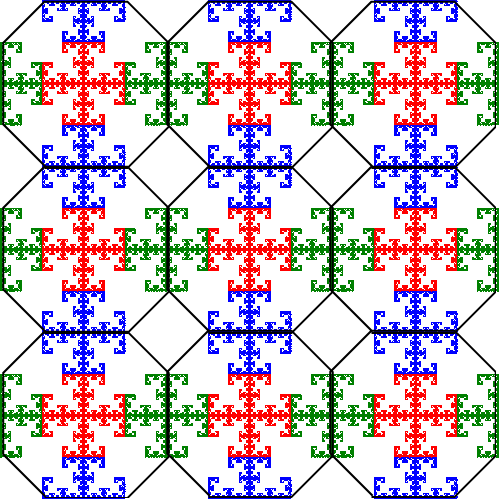
Notice that in the version without the tiles there are "holes" between the fractals (where the diamonds are located in the image with tiles). These can be filled with copies of the tiles scaled by 1/2 as illustrated in the following image.

Click the button below to see the effect of filling in all the holes with these 1/2 scaled tiles. But there are still some smaller square holes remaining! And these can be filled with copies of the tiles scaled by 1/4. Click the button to see the effect. And the process can be continued indefinitely to fill ever smaller holes with copies of the tiles scaled by 1/8, 1/16, etc.

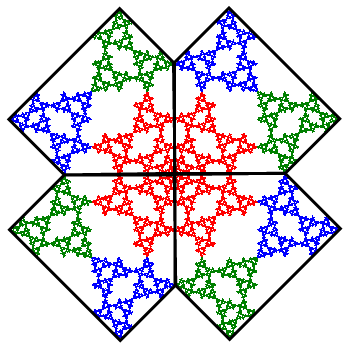
[Alternative View]
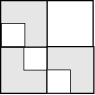
[Cross Stitch Design]
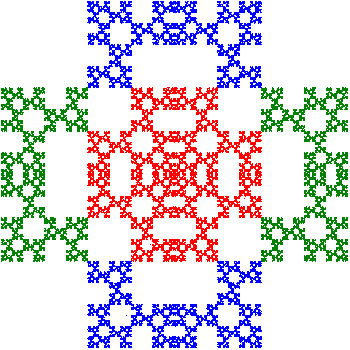
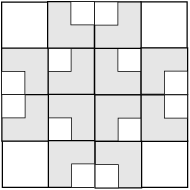
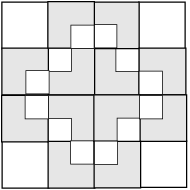
This tile can also be repeated in both the horizontal and vertical directions as shown below (with a slightly different coloring). And as with the relative 412 tiling, the holes between the tiles can be filled with scaled copies of the tiles. Click on the buttons to the left examine these effects.
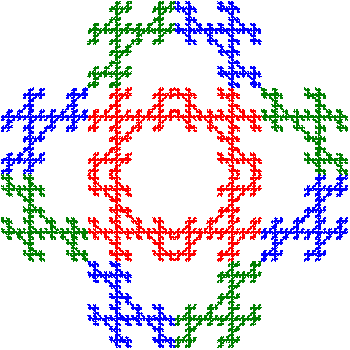
Here are examples of tiling with eight copies of Sierpinski relative 111, and four copies of Sierpinski relatives 313 and 333. Click on the tiles to see multiple copies (some scaled by 1/2) tiling the plane. For more examples, see the article by Taylor in the proceedings of the 2018 Bridges Conference.
 [Cross Stitch Design] |
|
Finally, you can even fill the holes in some of the Sierpinski relatives with copies of other Sierpinski relatives. Click here for a holiday inspired example using relatives 313, 214, and 111.
View some video demonstrations of these various tilings.
There are seven possible combinations for these symmetries: T, TG, TV, TR, THG, TRVG, and TRVGH. Some of these are illustrated below with symmetric Sierpinski relatives.
The following images use three different tilings of the convex hulls of Sierpinski relative 214. The first two can be classified as TV, i.e. they display translation and vertical reflection. The third has all five symmetries, so is labeled as TRVGH. Click on each image to toggle between the convex hulls and the frieze pattern.



The next image uses Sierpinski relative 111 to create a frieze pattern that has TRGV symmetries.
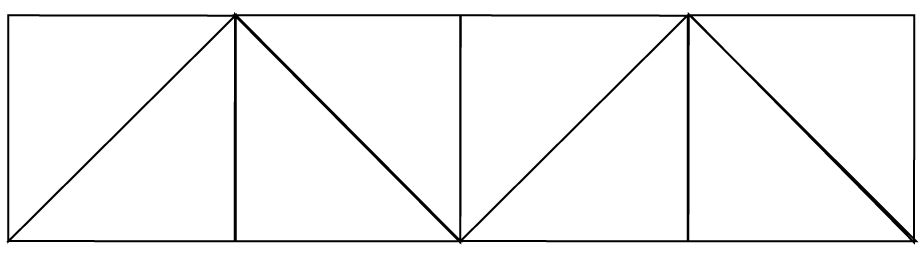
The next image uses the convex hull of Sierpinski relative 313 to create a frieze pattern that has TV symmetries.

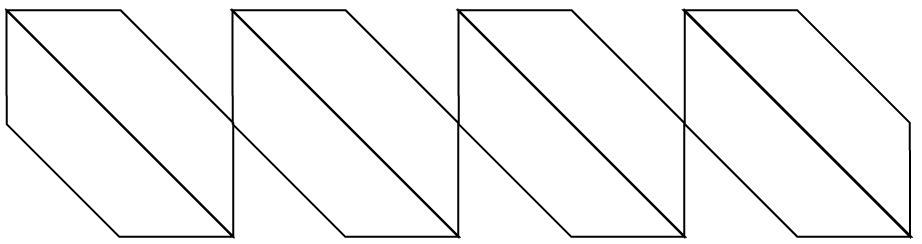
The next image uses the convex hull of Sierpinski relative 412 to create a frieze pattern that has TRVG symmetries.

The final image uses the convex hulls of Sierpinski relative 131 to create a frieze pattern that has TR symmetries.
Click here to see frieze designs in cross stitch. For other frieze examples, see Taylor's Bridges 2018 article.