Representing the Lévy Dragon Curve Symbolically

We consider the Lévy dragon curve as constructed using line segments starting with an initial horizontal segment. The left endpoint of this segment is considered the beginning of the curve. Let \(L_n\) denote the \(n\)th iteration. It consists of \(2^n\) segments and \(2^n-1\) corners. To get the next iteration, \(L_{n+1}\), each of the segments in \(L_n\) is replaced by two segments at right angles, always placing those segments towards the left of the segment in \(L_n\). Each iteration can be represented symbolically by a sequence consisting of the letters R L, S, and B. One can imagine moving along the individual segments making up the curve starting at the left endpoint. A corner is labeled R if the curve makes a right turn there of 90°, is labeled L if the curve makes a left turn of 90° at that corner, is labeled S if the curve continues straight at that corner (0° turn), and is labeled B if the curve make a 180° turn at that corner. The following image shows the symbolic coding for the first five iterations.

 
This construction can also be described by the following IFS:

\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {1/2} & { - 1/2} \\ {1/2} & {1/2} \\ \end{array}} \right]{\bf{x}}\)	scale by \(\frac{1}{{\sqrt 2 }}\), rotate by 45°
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/2} & { 1/2} \\ {-1/2} & { 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 0.5 \\ 0.5 \\ \end{array}} \right]\)	scale by \(\frac{1}{{\sqrt 2 }}\), rotate by −45°

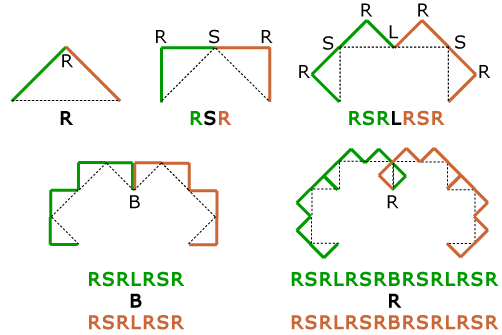
Notice that in these five examples, the beginning of \(L_{n+1}\) (shown in green) is the same sequence of letters as \(L_n\), then followed by an R, L, S, or B, which is then followed (in brown) by the sequence \(L_n\). This recursive pattern holds for all iterations since \[L_{n+1} = f_1(L_n) \cup f_2(L_n)\]

The first function in the iterated function system will just rotate \(L_n\) by 45° (which becomes the green pieces in the image above). This will not change the direction of the turn at each corner of \(L_n\), so the first half of \(L_{n+1}\) will have the same sequence of turns as \(L_n\). The second function in the IFS will rotate \(L_n\) by −45° (the brown piece) and then translate horizontally so that the beginning of the brown piece joins the tail of the green piece. But the brown piece is traversed in the same direction as the green piece, so the directions of the turns along the brown piece are the same as the directions of the turns along the green piece. (The IFS will also scale each piece, but this will not affect the direction of each turn.) Where the two pieces come together, we see that an R turn in \(L_n\) will produce an S turn in \(L_{n+1}\), an S turn in \(L_n\) will produce an L turn in \(L_{n+1}\), an L turn in \(L_n\) will produce a B turn in \(L_{n+1}\), and a B turn in \(L_n\) will produce an R turn in \(L_{n+1}\). This cyclic pattern R,S,L,B will continue.

We can express this relationship as \(L_{n+1} = L_nX_{n+1}L_n\) where
\(X_{n+1} = S \text{ if } X_n = R\)
\(X_{n+1} = L \text{ if } X_n = S\)
\(X_{n+1} = B \text{ if } X_n = L\)
\(X_{n+1} = R \text{ if } X_n = B\)

Since \(L_5\) = RSRLRSRBRSRLRSR R RSRLRSRBRSRLRSR with \(X_5 = R\), we know that \(L_6\) must start and end with this sequence of turns with an extra S added in the middle. So
\(L_6 = L_5SL_5\) = RSRLRSRBRSRLRSRRRSRLRSRBRSRLRSR S RSRLRSRBRSRLRSRRRSRLRSRBRSRLRSR

The image below shows \(L_6\) with the two copies of \(L_5\) colored green and brown. Where the colors change at the bottom of the square in the middle is the corner with code S. (The segment down to that square is traversed twice, once as green and then again as brown. This can be seen in the image of \(L_4\) above.)

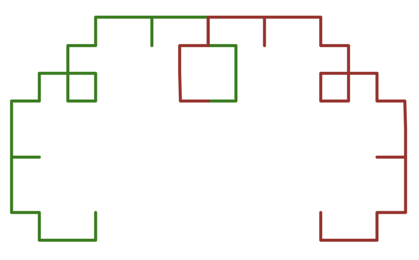
The curve can be traversed from the left endpoint to the right endpoint in groups of four segments corresponding to the code RSR (the same as \(L_2\) above). [Demonstration with \(L_9\) and \(L_{12}\)]

Building the code for higher order iterations can be done recursively using the algorithm described above. Fortunately there is another method that can give the code for \(L_n\) directly. It is based on the following two observations.

Let the turns at the corners of \(L_n\) be denoted by \(a_i\) for \(1 \le i \le m\) and let the turns at the corners of \(L_{n+1}\) be denoted by \(b_i\) for \(1 \le i \le 2m+1\), where \(m=2^n-1\).

1. The curve always starts with a right turn at the first corner, so \(b_1\) = R. \(L_{n+1}\) is obtained by replacing each of the segments in \(L_n\) with two segments at right angles. These are the odd-numbered corners in \(L_{n+1}\). Because the new segments are always placed towards the left of the previous iteration \(L_n\) , the angle at the new corners is always 90° to the right, as illustrated in the figure below. 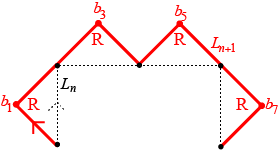Therefore the odd corners are all coded as R.
    
2. The even corner corresponding to \(b_{2k}\) in iteration \(L_{n+1}\) coincides with the corner corresponding to \(a_k\) in \(L_n\). The following image shows the four possible orientations for the segments in \(L_n\) and \(L_{n+1}\) at this common corner (the direction of the initial segment of \(L_n\) might be oriented differently, but this would not change the relative behavior of the other segments in the four figures.)

   

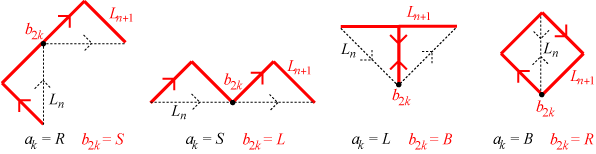
   Associate the ordered list (R,S,L,B) with the ordered list (0,1,2,3), so 0=R, 1=S, 2=L, and 3=B. Then the important observation is that in each case the turn at \(b_{2k}\) at this common corner is the value in the list for \(a_k\) shifted cyclically one position to the right, that is, \(b_{2k}=(a_k\ + 1) \text{ mod }4\) for \(1 \le k \le m\). We know, however, that \(L_{n+1}\) begins with \(L_n\) and therefore \(b_k = a_k\). This means that \(b_{2k}=(b_k\ + 1) \text{ mod }4\) for \(1 \le k \le m\).

These two observations provide an algorithm for how to generate the symbolic code for \(L_n\). For example, here is how it could be done for \(L_4\). Since \(2^4-1=15\), there are 8 odd-numbered corners in \(L_4\).

Write out 8 R's corresponding to the odd numbered corners, leaving space between them Now fill space 2 with the value in position 1 shifted 1 to the right in (R,S,L,B): Fill space 4 with the value in position 2 shifted 1 to the right in (R,S,L,B): Fill space 6 with the value in position 3 shifted 1 to the right in (R,S,L,B): Fill space 8 with the value in position 4 shifted 1 to the right in (R,S,L,B): Fill space 10 with the value in position 5 shifted 1 to the right in (R,S,L,B): Fill space 12 with the value in position 6 shifted 1 to the right in (R,S,L,B): Fill space 14 with the value in position 7 shifted 1 to the right in (R,S,L,B):

This is a convenient method to do by hand for small values of \(n\). For larger iterations, however, it is not difficult to write a short program to generate the code using the two observations above. [Python example]

Try it!
Iteration number (2 to 12)
n = Compute code Clear

The final method gives a way to calculate directly whether the \(r\)th turn is R, S, L, or B. Write \(r = k4^m\) where \(k\) is not a multiple of 4. As in method 2, associate 0=R, 1=S, 2=L, and 3=B.

• If \(k\) is odd, then \(b_r = 2m \text{ mod } 4\)
• If \(k\) is even, then \(b_r = (2m+1) \text{ mod } 4\)

Here is why that works.

Write \(r = k4^m=k2^{2m}\). Using the second observation in method 2, we can keep dividing by 2 until only \(k\) is left (if \(m =0\) then no divisions are needed.) Each time we divide by 2, we must also add 1 corresponding to the cyclical shift to the right in the list (R,S,L,B). \[b_r = b_{k2^{2m}} = (b_{k2^{2m-1}}+1) = (b_{k2^{2m-2}}+2) = \dots = (b_{k2^{0}}+2m) = (b_k + 2m) \text{ mod } 4\] If \(k\) is odd, then \(b_k = 0 \) and \(b_r = 2m \text{ mod } 4\). If \(k\) is even, then \(k = 2p\) where \(p\) is odd since \(k\) is not a multiple of 4. Therefore one more division by 2 yields \[b_r = (b_k + 2m) \text{ mod } 4 = (b_p + 1+2m) = (1+2m) \text{ mod } 4.\]

For example, in \(L_{10}\), which has 2047 corners, the direction at turn 2020 is L because \(2020=505 \cdot 4^1\) and 505 is odd, so \(b_{2020} = (2\cdot 1) \text{ mod }4 = 2\).

This method can be summarized in the following chart with \(r = k4^m\), \(k\) not a multiple of 4. [Explanation]

\(k\)	\(m\)	\(b_r\)
odd	even	R
even	even	S
odd	odd	L
even	odd	B

The Lévy dragon is equal to \(\displaystyle \lim_{n \rightarrow \infty} L_n\). Since each \(L_{n+1}\) begins with \(L_n\), it makes sense, as Knuth and Davis remarked in their article about the Heighway dragon, to express the Lévy dragon as the infinite sequence of R's, S's, L's, and B's obtained as each finite sequence for \(L_n\) is extended to the limit. Given any particular position in the infinite sequence, method 3 above can be used to determine whether the code in that position is R, S, L, or B.

Try it!

Position r = Compute