


The Koch snowflake can be constructed from either an equilateral triangle with Koch curves placed around the boundary pointing outwards, or from a regular hexagon with Koch curves placed around the boundary pointing inwards.
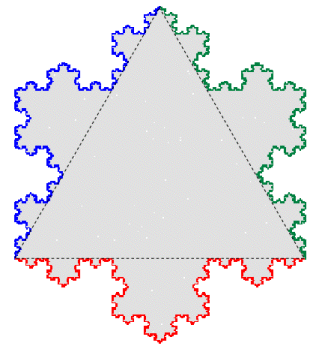
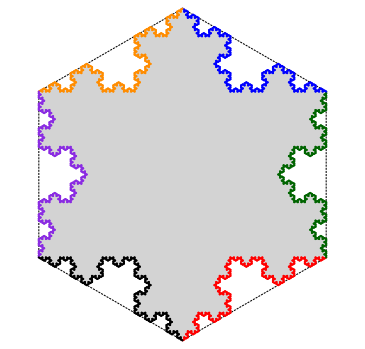
We can take a regular hexagon and place an equilateral triangle along one of its edges as shown below. If the first step in the iterative construction of the Koch snowflake is applied to both the hexagon and triangle, then the common side will be perfectly deformed outward from the triangle and inward for the hexagon. Click the image to toggle between the hexagon/triangle and the first iteration.
Continued iterations will result in two copies of the Koch snowflake that perfectly fit together along that common edge. Click on the image below to demonstrate this.

Now the plane can be tiled with copies of regular hexagons (in orange) and equilateral triangles (in green) as shown in the image below, where each hexagon shares its edges with an equilateral triangle. This is an example of a semiregular tessellation, or sometimes called an Archimedean tessellation. The iterative construction will, in the limit, deform each of the hexagons and each of the triangles into Koch snowflakes as illustrated above, thus providing a tiling of the plane. Click on the iterations to the left to see this in action.
Iteration

Here is a video illustrating the transformation of the semiregular tessellation into the tiling by Koch snowflakes.
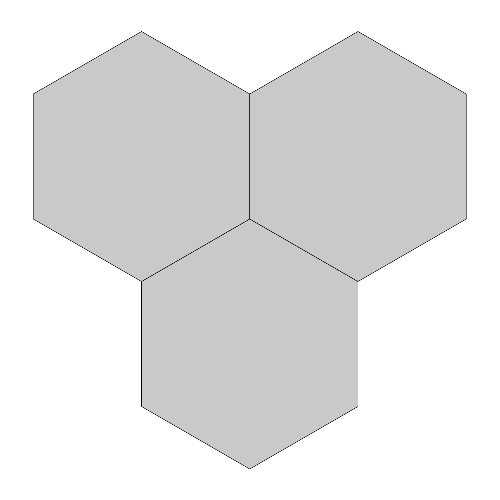
The plane can also be tiled just with copies of identical-sized hexagons. But if the Koch snowflake iteration is applied to this tiling, holes will appear. However, those holes can be filled with the Koch anti-snowflake! Trying clicking on the buttons below to see what happens.
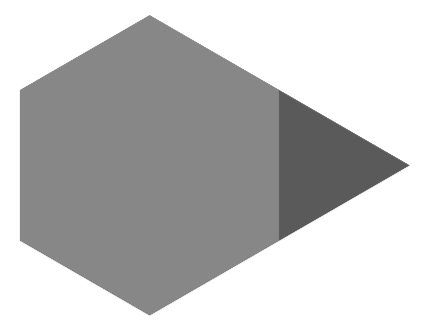
The reason that the anti-snowflake fills the holes between the snowflakes obtained from the hexagons is that the boundary of the anti-snowflake is formed by placing copies of the Koch curve along the boundary of the red equilateral triangle that overlays the three hexagons, as shown below. As the iterative construction for the Koch curves is applied to the hexagons and the equilateral triangle, the Koch curve iterates for the anti-snowflake will surround the holes generated by the hexagon iterations, and the respective Koch curve boundaries will converge together in the limit. Click on the buttons to the left to see what happens during the first four iterations.
Iteration
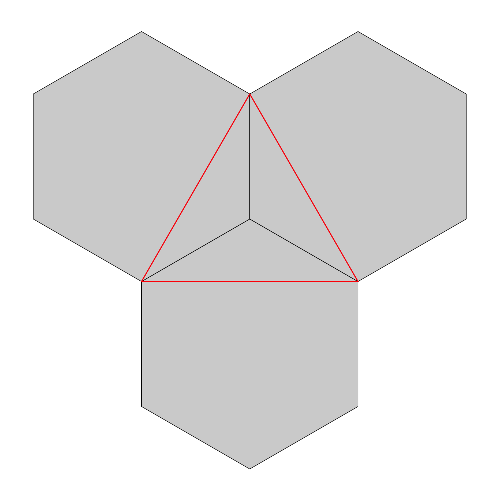
So we can tile the plane with regular hexagons (in yellow) overlaid with equilateral triangles (in green). The iterative construction will, in the limit, deform each of the hexagons into snowflakes and each of the triangles into anti-snowflakes that fill the holes as illustrated above, thus providing a tiling of the plane. Click on the iterations to the left to see this in action.
Iteration

Here is a video illustrating the transformation of the tiling of the plane by hexagons into a tiling by Koch snowflakes and anti-snowflakes.