


Construction
Video
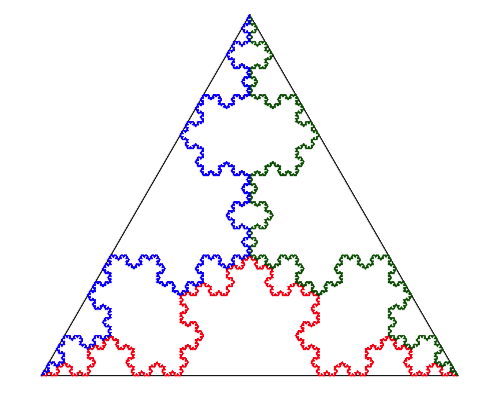
Iteration
Boundary
L-System
Animation
Angle 60
Axiom F++F++F
F —> F+F−−F+F
Construction
Animation
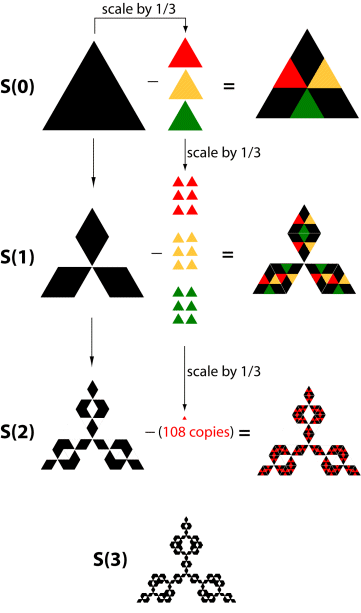
Continue this construction to get a decreasing sequence of sets \[ S(0) \supseteq S(1) \supseteq S(2) \supseteq S(3) \supseteq \cdots \] The intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often, lies inside the Koch anti-snowflake described above and its outer boundary is the same as that of the anti-snowflake.
IFS
Animation
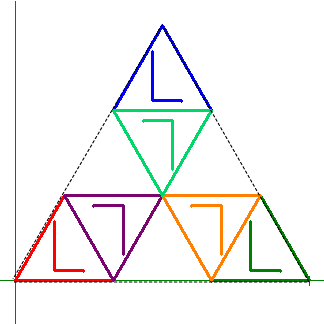
Other rotations are possible because of the symmetry of an equilateral triangle. Changing the rotation will likely change the translation for that function.
|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/3} & {0 } \\
{0} & { 1/3} \\
\end{array}} \right]{\bf{x}} \) |
scale by 1/3 |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/3} & {0} \\
{ 0} & { 1/3} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/3 } \\
{\sqrt 3 /3} \\
\end{array}} \right]\) |
scale by 1/3 |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 1/3} & {0} \\
{ 0} & { 1/3} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{2/3} \\
{0} \\
\end{array}} \right]\) |
scale by 1/3 |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ -1/3} & {0 } \\
{0} & { -1/3} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{1/2} \\
{\sqrt 3 /6} \\
\end{array}} \right]\) |
scale by 1/3, rotate by 180° |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ -1/3} & {0 } \\
{0} & { -1/3} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{5/6} \\
{\sqrt 3 /6} \\
\end{array}} \right]\) |
scale by 1/3, rotate by 180° |
|
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{- 1/3} & {0 } \\
{0} & { -1/3} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{2/3} \\
{\sqrt 3 / 3} \\
\end{array}} \right]\) |
scale by 1/3, rotate by 180° |
\[\sum\limits_{k = 1}^6 {{r^d}} = 1\quad \Rightarrow \quad d = \frac{{\log (1/6)}}{{\log (r)}} = \frac{{\log (1/6)}}{{\log (1/3)}} = \frac{{\log (6)}}{{\log (3)}} = 1.63093\]
The outside boundary consists of three copies of the Koch curve which has a fractal dimension of 1.26186.