Snowflake Curve

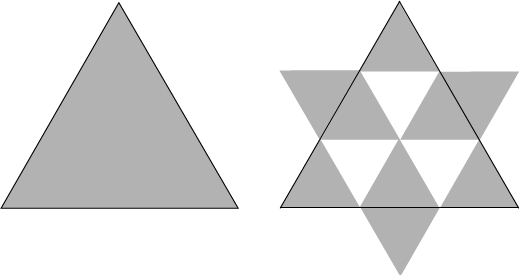
Start with an equilateral triangle. Divide the triangle into nine equal parts and place three of the scaled triangles outside the original triangle as illustrated in the figure above. This recursive procedure is continued and in the limit will produce the image of a snowflake.

The original equilateral triangle is scaled by 1/3. The first six copies are just translated and the other three are rotated by 60°, −60°, and 180°, then translated to the positions on the outside of the original triangle.
 

\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { 1/3} \\ \end{array}} \right]{\bf{x}} \)	scale by 1/3
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { 1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { 1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {2/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { 1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/6} \\ {\sqrt 3 /6} \\ \end{array}} \right]\)	scale by 1/3
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { 1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/2} \\ {\sqrt 3/6} \\ \end{array}} \right]\)	scale by 1/3
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { 1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {\sqrt 3 /3} \\ \end{array}} \right]\)	scale by 1/3
\({f_7}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/6} & {-\sqrt 3/6} \\ { \sqrt 3/6} & { 1/6} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/6} \\ {\sqrt 3/6} \\ \end{array}} \right]\)	scale by 1/3, rotate by 60°
\({f_8}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/6} & {\sqrt 3/6} \\ { -\sqrt 3/6} & { 1/6} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {2/3} \\ {\sqrt 3/3} \\ \end{array}} \right]\)	scale by 1/3, rotate by −60°
\({f_9}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/3} & {0} \\ { 0} & { -1/3} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {1/3} \\ {0} \\ \end{array}} \right]\)	scale by 1/3, rotate by 180°

4th Iteration
[Click for alternative image]

The first iteration has 9 triangles, 6 of which are inside the original triangle and 3 that are on the outside. The 3 outside triangles share an edge with 3 of the inside triangles, as can be seen in iteration 1 below. The recursive construction applied to the triangles with a common edge will result in overlapping triangles at the next iteration, as can be seen in the figure for iteration 2.

Iteration 1 9 Triangles	Iteration 2 75 Triangles

Because of the overlap, there are only 75 triangles in iteration 2 instead of the possible 9²=81 triangles. As more iterations are done, there will be more instances of overlapping triangles. The image below was drawn using the chaos game (random) algorithm with 2,000,000 points plotted and with the coloring based on pixel counting (shown in the chart on the right). The pixels in violet have been hit the most and reflect the effect of the overlapping triangles.

The total number of triangles in the nth iteration is given by the expression \[ T_n = \frac{(-2\sqrt{10}+5)(5-\sqrt{10})^n+(2\sqrt{10}+5)(5+\sqrt{10})^n}{10}. \] (Details)

Each of the triangles in the nth iteration has been scaled by (1/3)ⁿ, so if the original triangle has area 1, then each of these triangles would have area (1/3)²ⁿ = (1/9)ⁿ. Therefore the total area of the nth iteration is \[ A_n = \frac{T_n}{9^n} = \frac{1}{10}(-2\sqrt{10}+5)\left(\frac{5-\sqrt{10}}{9}\right)^n+\frac{1}{10}(2\sqrt{10}+5)\left(\frac{5+\sqrt{10}}{9}\right)^n. \] Here is a graph of \(A_n\) for the first 60 iterations.

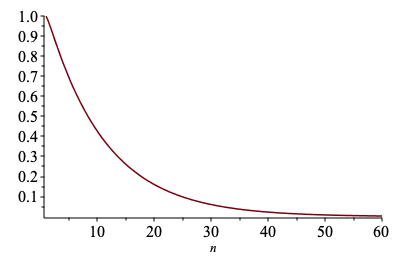
Since \[ 0 \lt \frac{5-\sqrt{10}}{9} \lt 1 \quad\quad \text{ and } \quad\quad 0 \lt \frac{5+\sqrt{10}}{9} \lt 1 \] then \(\displaystyle \lim_{n\rightarrow\infty}A_n = 0\), and so the area of the snowflake is 0.

The boundary of the snowflake is the same as the boundary of the Koch snowflake, and consists of three copies of the Koch curve. The snowflake lies inside of the Koch snowflake.

The snowflake curve is example 6.9 in Curious Curves by Darst, Palagallo, and Price in which they prove that if the fixed attractor of an iterated function system is connected, then the attractor is a curve. This snowflake is connected because each of the iterates in the construction of the snowflake is composed of connected sets, and thus the snowflake is a curve.

1. Richard Darst, Judith Palagallo, and Thomas Price. Curious Curves, World Scientific Publishing Company, 2010 [Preview available at Google Books]