

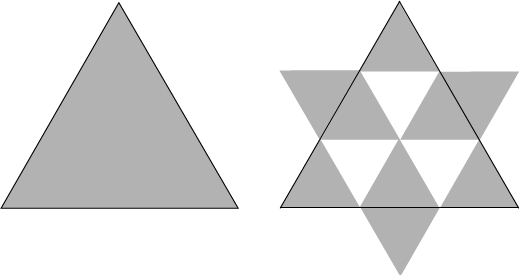
Start with an equilateral triangle. Divide the triangle into nine equal parts and place three of the scaled triangles outside the original triangle as illustrated in the figure above.
The first iteration has 9 triangles, 6 of which are inside the original triangle and 3 that are on the outside. The 3 outside triangles share an edge with 3 of the inside triangles, as can be seen in iteration 1 below. These form a parallelogram. The recursive construction applied to the triangles with a common edge will result in overlapping triangles at the next iteration, as can be seen in the figure for iteration 2.
 |
 |
| Iteration 1 9 Triangles | Iteration 2 75 Triangles |
Let \(s_n\) be the number of single triangles and \(d_n\) the number of parallelograms formed by double triangles sharing a common edge in the nth iteration. In iteration 1 above, \(s_1 = 3\) and \(d_1 = 3\). In iteration 2, \(s_2 = 15\) and \(d_2 = 30\). The figure below shows what happens to each single triangle and to each parallelogram when the next iteration is done.
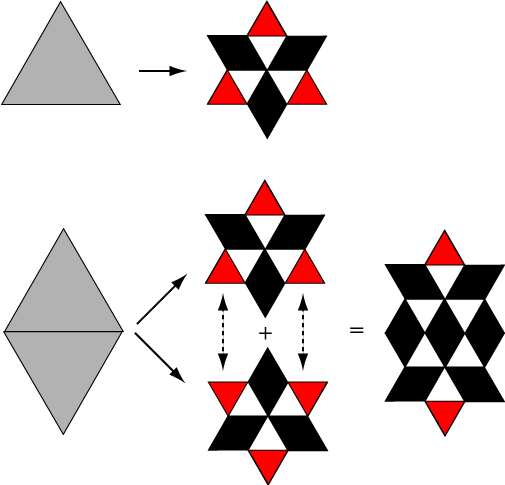
A single triangle will yield 3 new single triangles and 3 new parallelograms. A single parallelogram will yield 2 new single triangles and 7 new parallelograms. This can be summarized by writing \[ s_{n+1} = 3s_n + 2d_n \\ d_{n+1} = 3s_n + 7d_n \] or in matrix form \[ \begin{bmatrix} s_{n+1} \\ d_{n+1} \end{bmatrix} = \begin{bmatrix} 3 & 2 \\ 3 & 7 \end{bmatrix} \begin{bmatrix} s_{n} \\ d_{n} \end{bmatrix} \] for all \(n \ge 0\). Since the initial equilateral triangle (iteration 0) has \(s_0 = 1\) and \(d_0 = 0\), the solution to this recurrence relation is \[ \begin{bmatrix} s_{n} \\ d_{n} \end{bmatrix} = \begin{bmatrix} 3 & 2 \\ 3 & 7 \end{bmatrix} ^n \begin{bmatrix} 1 \\ 0 \end{bmatrix} \] The nth power of the matrix \(\displaystyle \begin{bmatrix} 3 & 2 \\ 3 & 7 \end{bmatrix}\) can be found using the eigenvalue decomposition of the matrix. The eigenvalues are \(-\sqrt10+5\) and \(\sqrt10+5\) with corresponding eigenvectors \(\displaystyle \begin{bmatrix} \frac{-\sqrt10-2}{3} \\ 1 \end{bmatrix}\) and \(\displaystyle \begin{bmatrix} \frac{\sqrt10-2}{3} \\ 1 \end{bmatrix}\). Therefore \( \begin{bmatrix} 3 & 2 \\ 3 & 7 \end{bmatrix} = QAQ^{-1} \) where \[ A = \begin{bmatrix} -\sqrt10+5 & 0 \\ 0 & \sqrt10+5 \end{bmatrix} \text{ and } Q = \begin{bmatrix} \frac{-\sqrt10-2}{3} & \frac{\sqrt10-2}{3} \\ 1 & 1 \end{bmatrix} \] Putting this all together gives \[ \begin{align*} \begin{bmatrix} s_{n} \\ d_{n} \end{bmatrix} &= \begin{bmatrix} 3 & 2 \\ 3 & 7 \end{bmatrix} ^n \begin{bmatrix} 1 \\ 0 \end{bmatrix} = QA^nQ^{-1}\begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ \\ &= \begin{bmatrix} \frac{-\sqrt{10}-2}{3} & \frac{\sqrt{10}-2}{3} \\ 1 & 1 \end{bmatrix} \begin{bmatrix} (-\sqrt{10}+5)^n & 0 \\ 0 & (\sqrt{10}+5)^n \end{bmatrix} \begin{bmatrix} \frac{-3\sqrt{10}}{20} & \frac{-\sqrt{10}+5}{10} \\ \frac{3\sqrt{10}}{20} & \frac{\sqrt{10}+5}{10} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ \\ &= \begin{bmatrix} \frac{1}{10}\left((\sqrt{10}+5)(5-\sqrt{10})^n+(-\sqrt{10}+5)(5+\sqrt{10})^n\right) \\ \frac{3\sqrt{10}}{20}\left((5+\sqrt{10})^n-(5-\sqrt{10})^n\right) \end{bmatrix} \end{align*} \] The total number of triangles in the nth iteration is \(T_n = s_n+2d_n\). Using the above result for \(s_n\) and \(d_n\) gives \[ T_n = \frac{(-2\sqrt{10}+5)(5-\sqrt{10})^n+(2\sqrt{10}+5)(5+\sqrt{10})^n}{10}. \]