



"Generating fractals can be an artistic endeavor, a mathematical pursuit, or just a soothing diversion."
Kerry Mitchell, from The Fractal Art Manifesto
Click on images to enlarge. All images are copyright © Larry Riddle. They are low resolution jpeg files and may not be used without permission.




This series of four counted cross-stitch pieces was inspired by a chapter from Chaos and Fractals: New Frontiers of Science. The Sierpinski Triangle is a fractal that can be generated by dividing a square into four equal subsquares, removing the upper right subsquare, and then repeating the construction on each of the three remaining subsquares. That is our "theme". The "variations" arise by exploiting symmetries of the square. The chapter in Chaos and Fractals describes 232 different images that can be made this way, of which I did 16 in counted cross stitch. The first images I chose to do are the only eight symmetric fractals (in this case a reflective symmetry across a 45° diagonal). The other eight were chosen either because they represented related variations or simply because they looked interesting. Each cross stitch piece is 12.5" x 12.5" and consists of 7 iterations of the fractal construction on 25 count per inch fabric. The first piece was displayed in the 2011 Exhibition of Mathematical Art at the Joint Mathematics Meeting and featured in the 2012 Calendar of Mathematical Imagery from the American Mathematical Society.
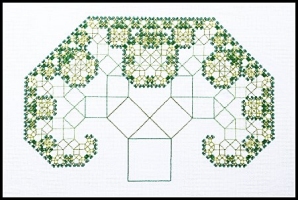
The fractals illustrated in the series above are known as Sierpinski relatives. The 12.5" x 12.5" cross-stitch pieces below contain multiple copies of the Sierpinski relatives shown in the first image of the series.
Each copy consists of 7 iterations of the fractal construction on 22 count per inch fabric. In the first piece, the four copies in the middle are reflections across the horizontal and vertical axes, and the four copies in the corners are rotations by 180°. In the second and third pieces, each of the four copies are rotated by 90° around a common center point. In the fourth piece, the four copies are reflections across the horizontal and vertical axes. The different colors in each piece are also meant to help illustrate the self-similarity of the fractal design. Ignoring the colors, all four pieces exhibit the eight symmetries of the square that form a finite group called the dihedral group of order 8. The second and third pieces were exhibited at the Juried Exhibit accompanying the AMS Special Session on Mathematics and Fiber Arts at the 2023 Joint Mathematics Meeting.
This 16" x 12" cross-stitch design on 28 count per inch fabric shows four frieze patterns, each made using 5 iterations of the same four Sierpinski relatives used above. A frieze pattern is an infinite strip with a repeating pattern that exhibits one or more of the following symmetries: translation (T), glide reflection G) , horizontal reflection (H), vertical reflection (V), and 180° rotation (R). The first and third friezes have TGVR symmetries, while the second and fourth have TV symmetries. For video demonstrations of these symmetries in these four frieze patterns, see Sierpinski Relative Frieze Demonstrations. This piece was part of the Mathematical Art Exhibition at the 2024 Joint Mathematics Meeting.
For more information about the mathematical construction of these fractals, see my section on Sierpinski Relatives that is part of my website on Classic Iterated Function Systems.



The Sierpinski carpet is constructed by first starting with a solid square, subdividing the square into nine congruent subsquares, and then removing the middle subsquare. The same procedure is then applied recursively to the remaining eight subsquares. The recursive construction is continued ad infinitum. The limiting set is the Sierpinski carpet. Rather than always removing the middle square, however, I wanted to replace that square with an image that would be scaled smaller and smaller at each iteration, in essence creating the mathematical complement of the Sierpinski carpet. After some experimentation, I found that round logos made perfect images for such a design. The Agnes Scott logos were a natural fit. The first two digital images were made using five iterations, thus resulting in 1+8+82+83+84 = 4681 copies of the logo in each picture.
The third piece, done in back stitch, is a relative of the Sierpinski Carpet. This time the square is rotated by 45° to form a diamond. It is again subdivided into nine congruent subsquares, but now the top three subsquares are removed while the two outer squares in the middle row are rotated 90° clockwise and 90° counterclockwise, respectively, and the bottom square is rotated 180°. The same procedure is then applied recursively to the remaining six subsquares, always taking into account the current orientation of a subsquare after being rotated. This back-stitch piece shows the result after five iterations. It consists of 6 self-similar pieces whose positions reflect the rotations done during each iteration. For more information about the mathematical construction of this fractal, see my section on Sierpinski Carpet Relatives that is part of my website on Classic Iterated Function Systems.

The traditional Pythagorean Tree fractal is constructed by starting with a square and constructing two small squares that enclose a right triangle with the original square along the hypotenuse. This construction is then applied recursively to each of the two smaller squares. The back-stitch design on the left shows the first 10 iterations of this construction (14" x 11" on 18 point canvas). The piece was stitched so that the new squares added at each iteration were done in different shades of green. The last set of squares (smallest in size) were done in dark green to show the development of the Lévy dragon (see next item) in the limit of the iterations. This image was part of the 2019 Exhibition of Mathematical Art at the Joint Mathematics Meeting.
When the Pythagorean tree is viewed as an iterated function system, one can start the construction with any image. For the digital print on the right I wanted to start with an actual picture of Pythagoras. I tweaked the functions in the iterated function system to use a rotation by 45° and a second rotation by 45° with a reflection. This gave a reflective symmetry for the trunk with two scaled images of Pythagoras looking at each other. I created the “leaves” with 500,000 points plotted using the random chaos game algorithm and colored based on the Barnsley "color stealing" algorithm. To give the leaves more realistic shading, the colors were stolen from a digital photograph of a field of green and yellow grass. This image was part of the 2012 Exhibition of Mathematical Art at the Joint Mathematics Meeting and was included in the 2014 Calendar of Mathematical Imagery from the American Mathematical Society. See the section on the Pythagorean Tree for more information.




The fractal now known as the Levy Dragon was first studied by Paul Levy in 1938, well before computers were able to draw the image or the name "fractal" had even been invented! The first image is that of the dragon done in counted cross stitch on 16 point canvas (10" x 8"). The two colors illustrate how the dragon is composed of two smaller self-similar copies. The second is the twelfth iteration of the dragon curve in back stitch on 22 count canvas (14" by 11"). The curve was done in blocks of the same shape (like a staple). The blocks alternate between two colors to make it easier to follow the path of the continuous curve from the beginning point on the left to the end of the curve on the right [see animated demonstration]. The Levy Tapestry consists of four copies of the Levy Dragon built from the edges of a square. There are two choices as one can orient the initial triangles used in the dragon construction to point inside the square or to point outside the square. The back-stitch design in the third image (12.5" x 12.5" on 10 point canvas) shows the twelfth iteration for the inside construction [see animated demonstration] while the last one on the right (12.5" x 12.5" on 18 point canvas) shows the twelfth iteration for the outside construction [see animated demonstration]. The outside tapestry was done in two shades of blue to better show each of the four copies of the Levy dragon. See Levy Dragon for more information. The two tapestry images were part of the 2016 Exhibition of Mathematical Art at the Joint Mathematics Meeting.

A symmetric binary tree is constructed by starting with a trunk that branches into two segments at a given angle, one to the left and one to the right, with each branch scaled by the same amount. Each branch is then split again according to the same angle and scaling ratio. This construction is iterated as many times as desired. This back-stitch design (12.5" x 12.5" on 18 count canvas) consists of four copies of 8 iterations of a symmetric binary tree with angle 45 ° and scaling ratio 1/sqrt(2), with the copies placed at 90° around a common center point. The branch tips of this binary tree (the points at the end of an infinite iteration of branches) is the Levy Dragon shown above.





The Heighway Dragon involves only a slight modification to the formulas that generate the Levy Dragon, yet the image is completely different. It was first investigated in 1966 by three physicists but was introduced to mathematicians by Martin Gardner in his Mathematical Games column of Scientific American. The first back-stitch design (14" by 11" on 18 count canvas) shows 12 iterations in the construction of the Heighway Dragon. The design starts at the "tail" on the left and alternates horizontal and vertical stitches until reaching the "head" at the right. The curve turns right at the end of each Red segment and turns left at the end of each bLue segment [see animated demonstration]. The second back-stitch design (14" by 11" on 18 count canvas, 14 iterations) illustrates that the Heighway Dragon is composed on an infinite union of geometrically similar components (shown in different shades of blue), any two of which intersect at no more than one cut point. One of the amazing properties of the Heighway Dragon is that despite its boundary being extremely non-smooth, four copies of the dragon fit exactly together around a central point. I tried to illustrate this mathematical idea in my back-stitch design (10" by 10" on 18 count canvas) that shows four copies of 12 iterations of the dragon in red, green, gold, and blue, each rotated by 90° as you go clockwise around the image. As before, each dragon can be traced starting at the center point as one continuous alternating sequence of vertical and horizontal stitches [see animated demonstration]. Two copies of a Heighway dragon placed back to back (so one is rotated 180°) will form a twindragon. The fourth back-stitch design (14' by 11" on 18 count canvas, 14 iterations) shows the twindragon with each Heighway dragon in a different shade of green [see animated demonstration]. The cross-stitch design on the far right (10" by 10" on 28 count canvas) shows how the twindragon can form a periodic tiling of the plane with translational symmetry. See Heighway Dragon for more information. The third and fifth images were part of the 2017 Exhibition of Mathematical Art at the Joint Mathematics Meeting.

A space filling curve is a continuous curve that passes through every point in a square. It is usually constructed mathematically as the limit of a sequence of piecewise linear curves. This back stitch piece (12.5" x 12.5" on 14 point canvas) shows the sixth iteration in the construction of a space filling curve described in the topology textbook by James Munkres. It can also be described as the sixth iteration of an iterated function system using four functions (reflected by the four colors in the design). The curve starts in the lower left corner and traces a continuous path through the red section into the blue section, then the orange section, and finally the green section, ending in the lower right corner. The curve intersects itself at many points but never crosses itself. The piece was stitched to follow this continuous path. Each of the four sections uses two alternating colors to illustrate the basic design of the iterated function system based on a triangular motif of 8 line segments turning at 45° angles. The motif is repeated over and over throughout the design with varying horizontal and vertical alignments. The "gaps" in the design would be filled in as more iterations are taken until in the limit all gaps would disappear and the square would be completely filled with four solid sections. This image was part of the 2015 Exhibition of Mathematical Art at the Joint Mathematics Meeting.

This algorithm for constructing this image starts with a horizontal line. That line is replaced by a motif consisting of 8 line segments as shown in this picture
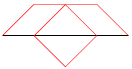
where the original line is in black and the 8 segments of the motif are in red. Each of the individual segments in the motif is now replaced by a scaled version of the motif to produce 64 new segments. This process is continued forever to produce a fractal, with the motif being scaled increasingly smaller at each step. This back stitch piece (14" x 11" on 22 point canvas) is what is obtained after 4 iterations. The colors are used to show the motif. The segments making up the square are in gold and the two segments before and two segments after the square are a dark red. Because of the way the iteration is done, the entire piece from the left beginning point to the right ending point can be traced by a continuous path (which overlaps itself in places). This is how the stitching was done, alternating the red and gold threads. This image was part of the 2019 Exhibition of Mathematical Art at the Joint Mathematics Meeting.

This piece (16" x 20" on 28 point canvas) was inspired by the website Gasket Fractals by Robert Fathauer. The black right triangle in the upper left corner is divided into nine similar right triangles. In the first two images, two triangles are removed as shown on the left and the construction is iterated on the seven remaining right triangles. In the bottom two images, three triangles are removed as shown on the left and the construction is iterated on the six remaining right triangles. The images on the right show the results after five iterations. The different colors in the four images are used to illustrate the self-similar nature of the resulting fractal. Each of the individual colored pieces of the fractal is a copy of the fractal scaled by 1/3. This piece was part of the 2021 Joint Mathematics Meeting virtual Exhibition of Mathematical Art.
See Right Triangle Divided by Nine on my Classic IFS website for more information.
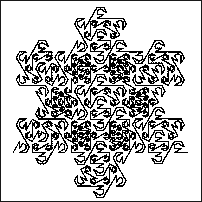

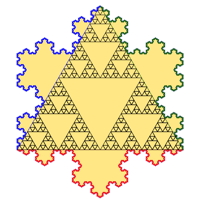
The Koch Snowflake, based on the Koch curve that appeared in 1904, is an example of a space filling curve. This means that the inside of the snowflake can be completely filled without any gaps by a mathematical curve that never crosses itself. It takes an infinite number of iterations to do this, however, so no computer image can ever show the actual curve! I tried to illustrate this mathematical idea with the digital print on the left that shows the fourth iteration of the construction using an iterated function system with 13 functions. The curve starts in the lower left corner and ends in the lower right corner. If you look closely you can trace the continuous path of this curve from beginning to end. The print shown in the middle is an image of the Koch snowflake that was drawn by plotting millions of points using the random chaos game algorithm and Michael Barnsley’s color stealing algorithm. The colors for the snowflake were stolen from a photograph of a fuchsia plant taken in Highlands, NC. The snowflake has been rotated to better fit the flowers. The image on the right is 5 iterations of the snowflake with a copy of 11 iterations of the Sierpinski triangle inside. It was drawn using turtle graphics in Python with my ColabTurtlePlus Python package. See Koch Snowflake for more information.
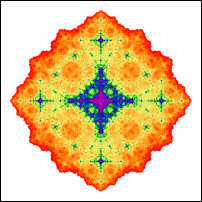


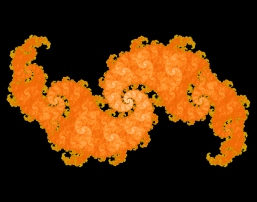
Symmetric fractals are formed using a single affine transformation or a given iterated function system, then modified using a cyclic or dihedral symmetry group. The image on the left is constructed by applying the elements of the D4 dihedral symmetry group to the iterated function system for the Koch curve. The second image was obtained by starting with a single affine transformation consisting of a scaling by 1/2, a rotation by 180°, and a translation by (0.5, 0.866), then given Z5 cyclic symmetry (rotations by 60°). The third image started with an iterated function system for a symmetric binary tree of angle 45° to which was then applied the elements of the Z4 cyclic group (rotations by 90°) to create a new iterated function system (the image also exhibits D4 symmetry). The last image comes from composing the elements of the Z2 cyclic group with the Golden Dragon fractal. The four images were colored using pixel counting in which the colors represent how many times a particular pixel in the image was plotted. Three of these images are featured in my article "Creating Symmetric Fractals" which appeared in Math Horizons, Vol. 24, No. 2 (November 2016) and was reprinted in The Best Writings on Mathematics 2017, Mircea Pitici, Editor, Princeton University Press. The last image was featured on the cover of the Math Horizons issue.




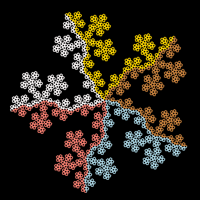

ColabTurtlePlus is a Python module that I wrote for drawing classic Turtle figures in Google Colab notebooks. It can be used to draw the fractals associated with iterated function systems that can be described using L-systems. The first image is the Peano-Gosper space-filling curve whose limit set is the flowsnake. The second and third images are 11 iterations of the Levy Inside and Levy Outside tapestries. The fourth image consists of four Heighway dragons (12 iterations) tiling the plane. The fifth image is the pentadentrite 2nd form fractal (4 iterations) and the last image is the McWorter pentigree 2nd form fractal (4 iterations). See the Python code on my ColabTurtlePlus Github site.