Classic Iterated Function Systems

Proofs for Pedal Triangles

In the following diagram, the points $A_1$, $B_1$, and $C_1$ are where the altitudes from each vertex of the acute $\triangle ABC$ intersect the opposite sides. Each of these altitudes makes an angle of 90° with the side of the triangle.

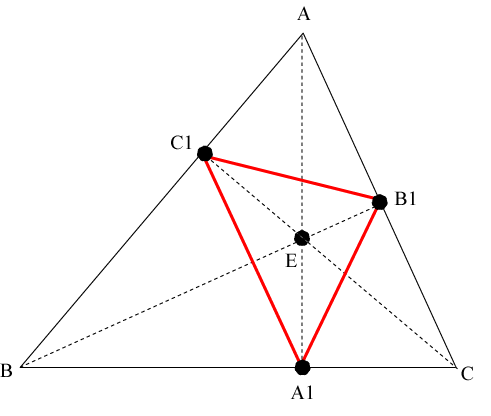
We want to show that $\triangle AB_1C_1$, $\triangle A_1BC_1$, and $\triangle A_1B_1C$ are similar to $\triangle ABC$. We will do this for $\triangle AB_1C_1$. The argument for the other two triangles are similar. It is only necessary to show that triangles $\triangle ABC$ and $\triangle AB_1C_1$ have the same angles. Since the vertex at A is common to both triangles, that angle is the same for both triangles. We now show that $\angle B = \angle AB_1C_1$.

First, notice that $\angle AEC_1 = \angle B$ because $\triangle ABA_1$ and $\triangle AC_1E$ are both right triangles that share the angle $\angle C_1AE$.

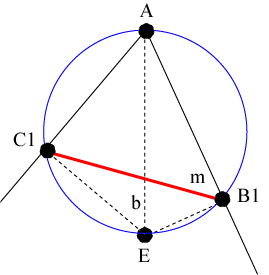
Let $b = \angle AEC_1$ and $m = \angle AB_1C_1$. We want to show that $b = m$. In the figure above, the three points $A$, $C_1$, and $E$ lie on a circle. Because $\triangle AC_1E$ is a right triangle, the segment $AE$ is a diagonal of this circle. Now the three points $A$, $B_1$, and $E$ also lie on a circle. Since $\triangle AB_1E$ is also a right triangle, the segment $AE$ is a diagonal of this circle. Thus both circles must be the same since they have the same diagonal. Thus all four points actually lie on the same circle as shown in the figure.
 

Lemma: Let points $P$, $R$, and $S$ lie on a circle with center $O$. In the figure below, if the chords $SR$ and $SP$ form the same arc as the chords $OR$ and $OP$, then the central angle $n$ is twice the inscribed angle $s$.

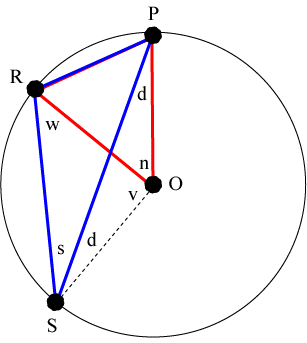
To see why this is true, first notice that triangles $\triangle ORS$ and $\triangle OPR$ are isosceles triangles. Also observe that $2d+n+v = 180^\circ$ and $2w+v = 180^\circ$ (since $s+d = w$). Subtracting these two equations shows that $2(d-w) + n = 0$, or $2(w-d) = n$. But $w-d = s$, so we get $2s = n$.

 
Now apply the lemma to the situation above. Since both sets of chords from points $E$ and $B_1$ form the same arc $AC_1$ of the circle, the lemma implies that both angles are half the central angle with that arc, and hence $b = m$.

Consider again the picture of the pedal triangle. We want to know the scaling factor relative to the original triangle for each of the similar triangles left when the pedal triangle is removed .

Since $\triangle ABC$ is similar to $\triangle AB_1C_1$, the corresponding sides are proportional, i.e.

\[\frac{{A{B_1}}}{{AB}} = \frac{{A{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\]

But $\triangle ABB_1$ is a right triangle, so $\cos(A) = AB_1/AB$. Thus the scaling factor for the top triangle is $\cos(A)$. The same argument shows that the scaling factor for the lower left triangle is $\cos(B)$ and the scaling factor the lower right triangle is $\cos(C)$.

The IFS for the Sierpinski pedal triangle involves scaling, reflections, rotations, and translations. We can take the original triangle so that vertex $B$ is at the origin and vertex $C$ is at the point $(1,0)$. The triangle is then completely specified by the values of the three angles $A$, $B$, and $C$.

Consider the following example.

 

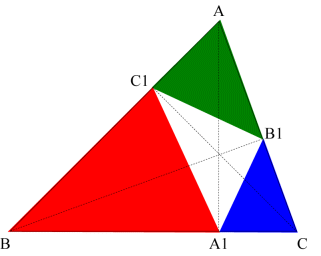
The scaling factor, as shown above, for the red triangle is $\cos(B)$. The first step is to scale the original triangle by $\cos(B)$.

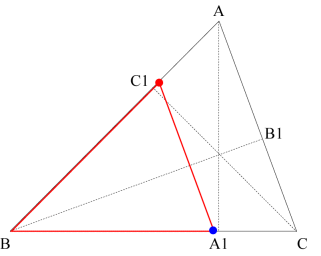
Now $\triangle ABC$ is similar to $\triangle A_1BC_1$ as shown in the first section above. Thus the red point must go to point $A_1$ and the blue point must go to $C_1$. To do this, first do a vertical reflection across the x-axis followed by a counterclockwise rotation through the angle $B$. No additional translation is needed.

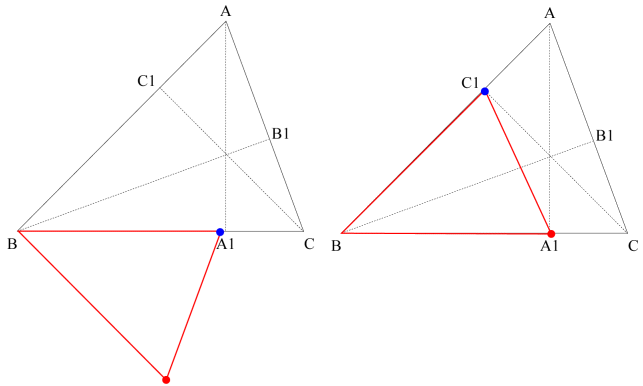
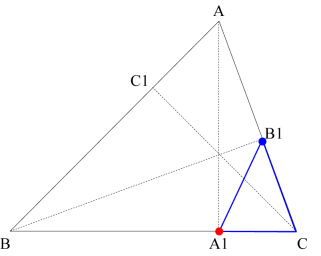
The scaling factor for the blue triangle is $\cos(C)$. Scale the original triangle by $\cos(C)$.

Since $\triangle ABC$ is similar to triangle $\triangle A_1B_1C$, the red point must go to $A_1$ and the blue point must go to $B_1$. To do this, first do a vertical reflection across the x-axis followed by a clockwise rotation through the angle $C$.

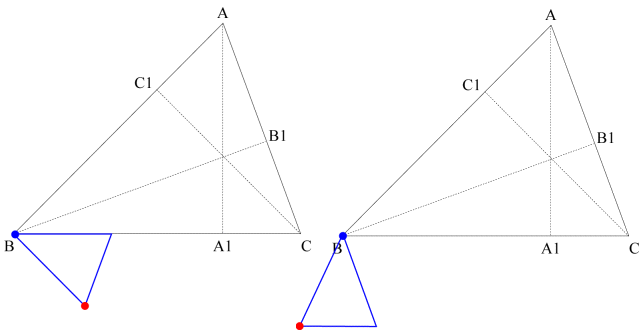
The final step is to translate the triangle so that the blue point goes to $B_1$. To find the coordinates $(x,y)$ of $B_1$, first notice that \({B_1}C = BC \cdot \cos (C) = \cos (C) \) and therefore

\[\begin{align} x &= 1 - {B_1}C \cdot \cos (C) = 1 - {\cos ^2}(C) = {\sin ^2}(C) \\ y &= {B_1}C \cdot \sin (C) = \sin (C)\cos (C) \\ \end{align}\]

The scaling factor for the green triangle is $\cos (A)$. Scale the original triangle by $\cos (A)$.

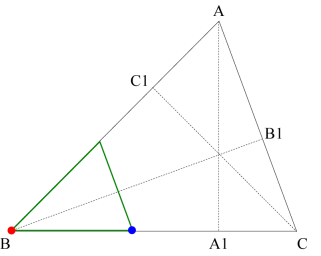
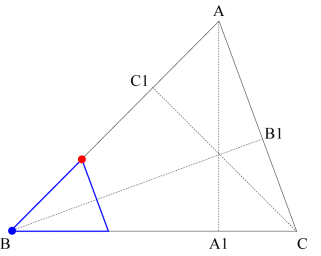
Since $\triangle ABC$ is similar to $\triangle AB_1C_1$, the red point must go to $B_1$ and the blue point must go to $C_1$. To do this, first do a horizontal reflection across the y-axis.

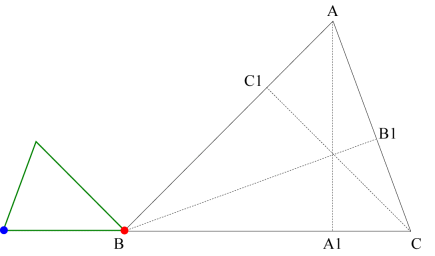
Now we need to rotate the green triangle so that the side from the top vertex to the origin becomes parallel to side $AC$. As the following figure shows, this involves rotating the green triangle clockwise through the angle $C-B$. (If $C \lt B$, then the rotation would be counterclockwise through the angle $B-C$.)

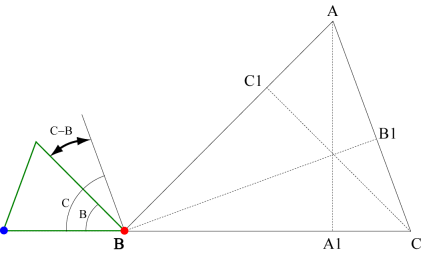
The final step is to translate the green triangle so that the red point goes to point $B_1$. This translation is the same as for the blue triangle.

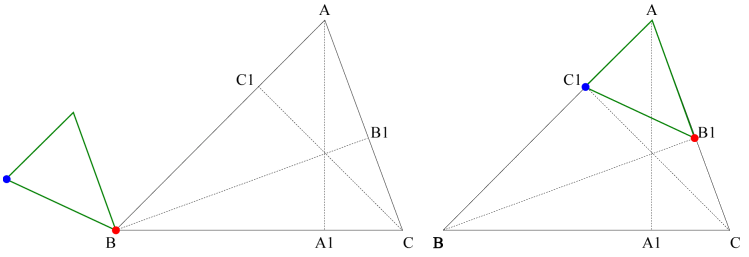
Note: If the length of line segment $BC$ is not equal to 1, then the translation vector should be multiplied by the length of segment $BC$.

The following video shows an animation that summarizes the steps in the iterated function system for generating a Sierpinski pedal triangle.