Classic Iterated Function Systems

Larry Riddle, Agnes Scott College

2nd Form of McWorter's Pentigree


Description

 
 


Animation
Start with a pentagon with sides of length 1. Along each side, construct the basic motif for a McWorter pentigree. These five copies fit nicely together to form six smaller pentagons as shown in the figure below, where each motif is shown in a different color. Continue the pentigree construction along each side.

A central pentagon with 5 equivalent pentagons placed at each of its vertices

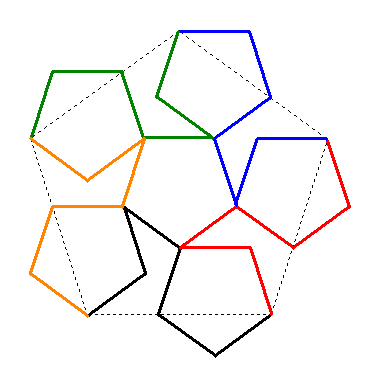
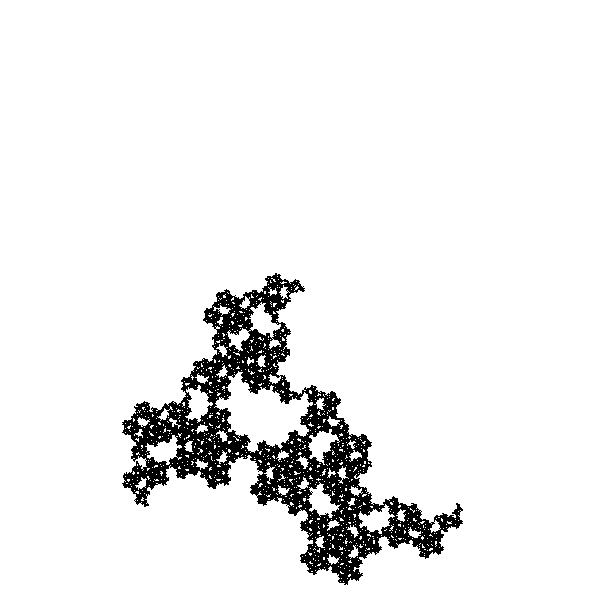
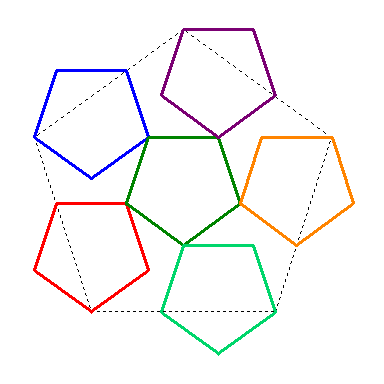
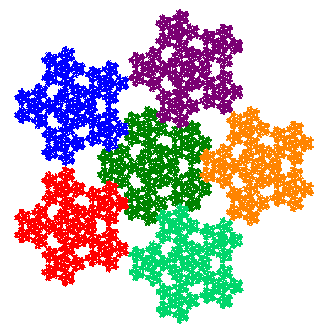
You can also see how five copies of the McWorter pentigree fit together by successively adding copies using the buttons below, or by viewing the L-system animation farther down.

One copy of pentigree with the buttons adding 4 additional copies around a common point

Iterated
Function
System

 
 


IFS
Animation
An alternative view of the 2nd form of McWorter's pentigree is to consider each of the six pentagons as a scaled version of the unit pentagon with an appropriate rotation and translation as shown in the figure below. Because of the symmetry of the pentagon, it is possible to rotate them in various ways and still create the same image. Here we rotate each scaled pentagon by 36°.

The scaling factor is still $r$ = 0.381966. This leads to the following iterated function system [IFS Details]:
 
\({f_1}({\bf{x}})= \left[\begin{array}{rr} 0.309 & -0.255\\ 0.255 & 0.309 \end{array}\right]{\bf{x}}\)
scale by $r$, rotate by 36°
\({f_2}({\bf{x}})= \left[\begin{array}{rr} 0.309 & -0.254\\ 0.254 & 0.309 \end{array}\right]{\bf{x}} + \left[\begin{array}{r} 0.727\\ 0 \end{array}\right]\)
scale by $r$, rotate by 36°
\({f_3}({\bf{x}})= \left[\begin{array}{rr} 0.309 & -0.255\\ 0.255 & 0.309 \end{array}\right]{\bf{x}} + \left[\begin{array}{r} 0.225\\ 0.691 \end{array}\right]\)
scale by $r$, rotate by 36°
\({f_4}({\bf{x}})= \left[\begin{array}{rr} 0.309 & -0.255\\ 0.255 & 0.309 \end{array}\right]{\bf{x}} + \left[\begin{array}{r} -0.588\\ 0.427 \end{array}\right]\)
scale by $r$, rotate by 36°
\({f_5}({\bf{x}})= \left[\begin{array}{rr} 0.309 & -0.255\\ 0.255 & 0.309 \end{array}\right]{\bf{x}} + \left[\begin{array}{r} -0.588\\ -0.427 \end{array}\right]\)
scale by $r$, rotate by 36°
\({f_6}({\bf{x}})= \left[\begin{array}{rr} 0.309 & -0.255\\ 0.255 & 0.309 \end{array}\right]{\bf{x}} + \left[\begin{array}{r} 0.225\\ -0.691 \end{array}\right]\)
scale by $r$, rotate by 36°

Similarity
Dimension

We have a hyperbolic IFS with each map being a similitude of ratio $r \lt 1$. Therefore the similarity dimension, $d$, of the attractor of the IFS is the solution to

\[\sum\limits_{k = 1}^6 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/6)}}{{\log (r )}} = 1.86172\]

L-System


L-system
Animation
3 iterations
 

L-system
Animation
4 iterations
The following L-system draws the 2nd form of McWorter's pentigree by constructing five copies of the pentigree around the sides of a regular pentagon as described in the description above.

Angle 36
Axiom F++F++F++F++F
F —> +F++F−−−−F−−F++F++F−

4 iterations

 

References

  1. Edgar, Gerald A. Measure, Topology, and Fractal Geometry, Springer-Verlag, 1990.