


The Heighway dragon now appears in different horizontal and vertical orientations depending on how it is drawn.
Scaling factor \(r = \frac{1}{\sqrt 2}\)
| First 2 iterations | Dragon | IFS |
| |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}}\) scale by r, rotate by 45° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { - 1/2} & { - 1/2} \\ {1/2} & { - 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 1 \\ 0 \\ \end{array}} \right]\) scale by r, rotate by 135° |
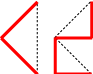 |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { - 1/2} \\
{1/2} & {1/2} \\
\end{array}} \right]{\bf{x}}\) scale by r, rotate by 45° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { - 1/2} & { - 1/2} \\ {1/2} & { - 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right]\) scale by r, rotate by 135° |
| First 2 iterations | Dragon | IFS |
| |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/2} & { -1/2} \\
{1/2} & { - 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
-1/2 \\
\end{array}} \right]\) scale by r, rotate by 135° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/2} & { -1/2} \\ {1/2} & { 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 1/2 \\ -1/2 \\ \end{array}} \right]\) scale by r, rotate by 45° |
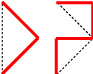 |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/2} & { -1/2} \\
{1/2} & { - 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
1/2 \\
\end{array}} \right]\) scale by r, rotate by 135° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/2} & { -1/2} \\ {1/2} & { 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 1/2 \\ 1/2 \\ \end{array}} \right]\) scale by r, rotate by 45° |
| First 2 iterations | Dragon | IFS |
| |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { 1/2} \\
{-1/2} & {1/2} \\
\end{array}} \right]{\bf{x}}\) scale by r, rotate by −45° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { - 1/2} & { 1/2} \\ {-1/2} & { - 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 1 \\ 0 \\ \end{array}} \right]\) scale by r, rotate by −135° |
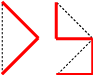 |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{1/2} & { 1/2} \\
{-1/2} & {1/2} \\
\end{array}} \right]{\bf{x}}\) scale by r, rotate by −45° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { - 1/2} & { 1/2} \\ {-1/2} & { - 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right]\) scale by r, rotate by −135° |
| First 2 iterations | Dragon | IFS |
| |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/2} & { 1/2} \\
{-1/2} & { - 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
1/2 \\
1/2 \\
\end{array}} \right]\) scale by r, rotate by −135° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/2} & { 1/2} \\ {-1/2} & { 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} 1/2 \\ 1/2 \\ \end{array}} \right]\) scale by r, rotate by −45° |
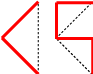 |
 |
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ - 1/2} & { 1/2} \\
{-1/2} & { - 1/2} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
-1/2 \\
1/2 \\
\end{array}} \right]\) scale by r, rotate by −135° \({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { 1/2} & { 1/2} \\ {-1/2} & { 1/2} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} -1/2 \\ 1/2 \\ \end{array}} \right]\) scale by r, rotate by −45° |
Each of the seven "chapters" of Jurassic Park starts with an iteration of the Heighway dragon (and a quotation from Ian Malcolm, the mathematician in the novel). The first three are in a vertical orientation and the last four are in a horizontal orientation.
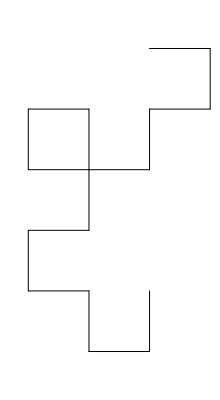 First Iteration |
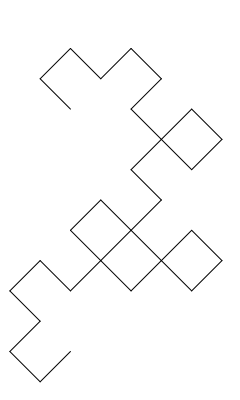 Second Iteration |
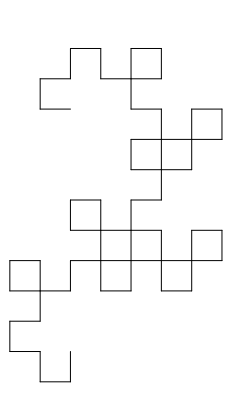 Third Iteration |
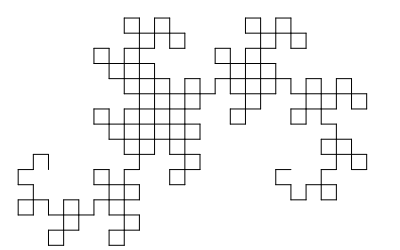 Fourth Iteration |
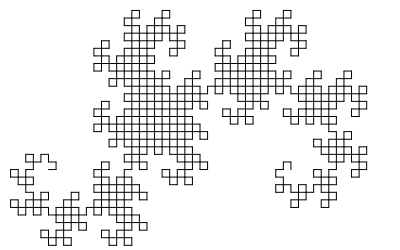 Fifth Iteration |
 Sixth Iteration |
 Seventh Iteration |
These actually come from a mixture of three different iterated function systems! The First Iteration is the 4th iterate of this website's IFS with adjusted translation vectors to make it vertical rather than horizontal. The Second Iteration and the Third Iteration are the 5th and 6th iterates, respectively, of the IFS corresponding to the William Harter's booklet cover, again with adjusted translation vectors to make them vertical. And finally, the Fourth through Seventh Iterations are, respectively, the 8th, 10th, 12th, and 14th iterates of the IFS for the version of the dragon from the Knuth-Davis article.