Classic Iterated Function Systems

Golden Dragon

Construction via line segments

Begin with a line segment. For the first iteration, replace this segment with two segments, the first scaled by $r$ and the second scaled by $r^2$, where $r$ is equal to $(1/\phi)^{1/\phi}$ with $\phi$ being the golden ratio, i.e. \(\phi = \frac{{1 + \sqrt 5 }}{2}\). The new segments are positioned in such a way that the original segment would have been the third side of the triangle formed by the new segments. Following along the original segment, we place the two new segments to the left. For the second iteration, replace the first segment with two new segments scaled in order by $r$ and $r^2$ and placed to the left. Replace the second segment from the first iteration with two new segments scaled in order by $r^2$ and $r$ and placed to the right. Continue this construction, always alternating the new segments between left and right along the segments of the previous iteration, and alternating the scaling order between ($r$, $r^2$) and ($r^2$, $r$). This generates the "golden dragon curve". The following figure shows the first three iterations for this construction.

To think of this construction as a result of affine transformations, consider the first iteration of the line segment from (0,0) to (1,0) as shown by the two red line segments in the following figure.

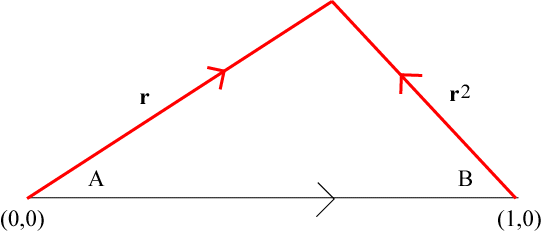
Remember that \(r = {\left( {\dfrac{1}{\phi }} \right)^{\frac{1}{\phi }}} = 0.74274\) where \(\phi = \dfrac{{1 + \sqrt 5 }}{2} = 1.618033988\).

We can use the Law of Cosines to determine the value of the angle A.

\[{r^4} = 1 + r^2 - 2r\cos A \Rightarrow \cos A = \frac{1 + r^2 - r^4}{2r} = 0.839678466\]

Therefore $A =\cos^{-1}(0.839678466) = 32.893818^\circ$. A similar calculation with the Law of Cosines for angle B shows that

\[B = \cos ^{-1}\left( \frac{1 + r^4 - r^2}{2r^2} \right) = 46.98598225^\circ \]

Because of the need to alternate left and right when constructing the dragon, we need to think of constructing the second line segment by a rotation through $180-B = 133.0140178^\circ$ followed by a translation of the origin to the point (1,0). This yields the following IFS.

The attractor of this IFS will be the golden dragon curve. The golden dragon consists of two self-similar pieces corresponding to the two functions in the IFS.

[Enlarge]

The golden dragon is self-similar with 2 non-overlapping copies of itself, one scaled by the factor $r$ and the other by the factor $r^2$. Therefore the similarity dimension, $d$, of the attractor of the IFS is the unique solution to \({r^d} + {r^{2d}} = 1\). To see that $d$ is the golden ratio $\phi$, you need to first recall that $\phi$ satisfies $\phi^2-\phi-1=0$, and hence $\phi^2=\phi+1$. Therefore \[{r^\phi } + {r^{2\phi }} = \frac{1}{\phi } + \frac{1}{{{\phi ^2}}} = \frac{{\phi + 1}}{{{\phi ^2}}} = 1\]

If two copies of the golden dragon are drawn vertically, with one reflected horizontally across a vertical line, they fit together nicely to form the following picture.