All these images were created with IFS Construction Kit. Click on an image for a larger view. Click on the corresponding ifs file to view the functions systems, or download the file so you can open it in IFS Construction Kit.
Sierpinski converging to his triangle |
 Durer's Pentagons |
 Barnsley's Spleenworth Fern |
Examples from Gerald Edgar, Measure, Topology, and Fractal Geometry, Springer-Verlag, 1990. [ifs file]
 Heighway Dragon |
 Twin Dragon |
 Levy Dragon |
 McWorter's Pentigree Dragon |
 Pentadentrite |
 Eisenstein Fractions |
 Barnsley's Wreath |
 Koch Snowflake |
Examples from Kevin Lee and Yosef Cohen, Fractal Attraction: A Fractal Design System for the Macintosh, Academic Press, 1991. [ifs file]
 Eiffel Tower |
 Nautilus |
 Spiral 1 |
 Spiral 3 |
 Square Snowflake |
 Starfish |
Examples of tilings from "Fractal Tilings in the Plane," Richard Darst, Judith Palagallo, and Thomas Price, Mathematics Magazine, Vol. 71, No. 1, February 1998, 12-23. [ifs file]
 Horizontal Tiling |
 Terdragon Tiling |
 Gosper Snowflake Tiling |
 4-rep Tile |
 4-rep Tile with Symmetry |
 5-rep Tile with Symmetry |
Examples from "Number Systems With a Complex Base: A Fractal Tool for Teaching Topology," Daniel Goffinet, American Mathematical Monthly, Vol. 98, No. 3 (March 1991), 249-255. [ifs file]
 b = −0.62e2π/7 |
 b = −0.697e2π/5 |
 b = 0.2+0.6i |
 b = 0.5 + 0.5i |
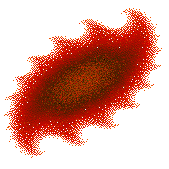 b = 0.8 + 0.2i |
 b = 0.65 − 0.3i |
Examples of Triangle Fractals motivated by Fractal World by Dave Ryan (website no longer available) [ifs file]
 Sierpinski Triangle |
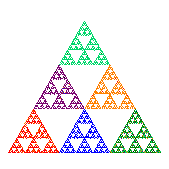 3 row triangle Triangle |
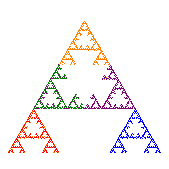 3 row fractal with rotations |
 4 row triangle fractal |
 2 rows with reflective symmetry |
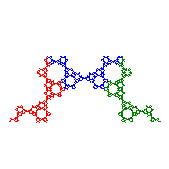 Opposite reflective symmetry |
Examples from Paul Bourke's website on fractals and chaos [ifs file]
 Chaos |
 Leaf |
 Maple Leaf |
 Spiral |
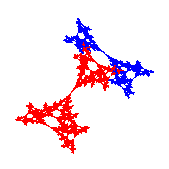 Mandelbrot like |
 Tree |
 Tree |
Examples of color stealing
 Input Image |
 Heighway Dragon |
 Input Image |
 Snowflake |
 Input Image |
 Fern |
 Input Image |
 Spiral |
 Input Image |
 Koch Snowflake |
Examples of fractal ferns from Ferns of the Canberra Region, a website maintained by David Nicholls and Christopher Nicholls. [ifs file]
 Barnsley's Fern (modified pinnae) |
 Culcita (=Calochlaenia) dubia Fern |
 "Fishbone" Fern |
 Cyclosorus Fern |
Examples of Pythagorean Trees
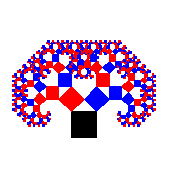 45 degrees |
 60 degrees |
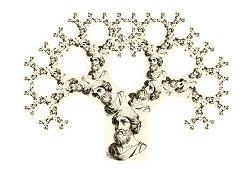 Pythagorus as a 45 degree tree! |
 The tips of a 10 degree tree |
Examples of Koch Curves with n-gons [ifs file]
 (4,1/3)-Koch Curve |
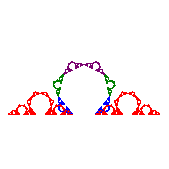 (7,0.15)-Koch Curve |
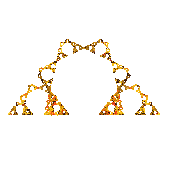 (7,0.20)-Koch Curve |
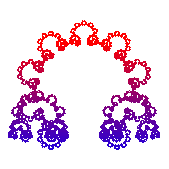 (10,1/5)-Koch Curve |
Examples of Fractal Movies. Click on an image to start the movie. All of these were constructed using the Fractal Movie Creator in IFS Construction Kit.
 Heighway Dragon to Sierpinski Triangle |
 Dancing Heighway Dragon |
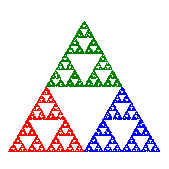 Sierpinski Triangle to Fern |
 Dancing Sierpinski |
 Rotating Starfish |
Examples of Symmetric Fractals using a single affine transformation or a given IFS, then modified using a cyclic or dihedral symmetry group. For an explanation of how these were created, see the Help section. [IFS file]
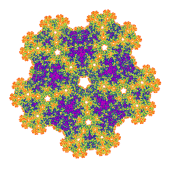 Z5 Symmetry |
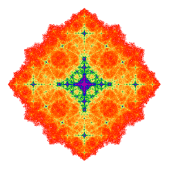 Koch curve using D4 symmetry group |
 Stained Glass Window (with Z6 Symmetry) Stained Glass Window (with Z6 Symmetry) |
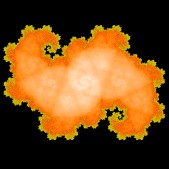 Heighway Dragon using Z2 symmetry group Heighway Dragon using Z2 symmetry group |
The following examples are from Symmetry in Chaos: A Search for Pattern in Mathematics, Art and Nature byMichael Field and Martin Golubitsky, Oxford University Press (Edition 1, 1992/95) and SIAM (Edition 2, 2009) [IFS file]
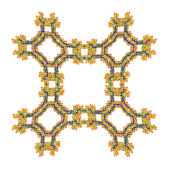
Astigmatism (D4) |
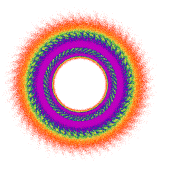 Cashmire (Z50) |
 Catherine Wheel (Z9) |
 Doily (D8) |
 Fifty Nations (Z50) |
 Sierpinski Pentagon (Z5) |
 Snowflake (D6) |