Individualized Computer Investigations For Multivariable Calculus

Larry Riddle
Department of Mathematics
Agnes Scott College
Decatur, GA 30030
LRiddle@agnesscott.edu

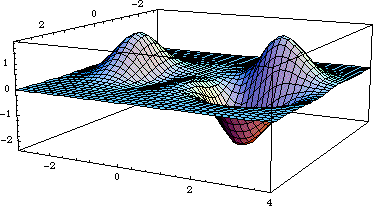
Picture of My Surface

Abstract

Sheldon Gordon has described several investigations that he has calculus students perform on polynomials whose coefficients are determined by the digits of the students' social security numbers. He remarks that the use of individualized projects are designed to get the students to take a personal interest in the topic under study and that the students seem to enjoy these types of investigations. In this note I would like to build upon this theme by describing a project that I have used in multivariable calculus classes.

The goal of the project is to investigate a function of two variables built from a student's social security number. The digits ABC-DE-FGHI of the number are taken mod 3 (to keep them small) and substituted into the following template

Surface formula

The student must investigate her (non-trivial) function to give a general description of what the surface looks like, determine the number and approximate locations of all local maximas, minimas and saddle points, and find the location and value of the absolute maximum and the absolute minimum. Moreover, she is asked to compute the maximum and minimum values of her function along the unit circle. My students enjoy this assignment more than traditional homework problems because of its individual nature and because of the interesting phenomena that can occur. It is not unusual for a student to proudly show off her surface and describe its features.

[htm icon] View paper in HTML format.
[pdf icon] View paper in Adobe Acrobat format.

Published in the College Mathematics Journal, Vol. 26, No. 3 (1995), 235-237.
Other Publications | My Home Page |

Last modified: August 2000