


"Fifth, you can combine pentagons in the following manner: First draw a pentagon and place pentagons of the same size on each side. Then place five pentagons on their sides, particularly along the two sides. This will result in the formation of five narrow lozenges between them. Then add pentagons in the angles which will have formed, so that these will touch the narrow lozenges with their corners. You can continue in this manner as long as you desire."
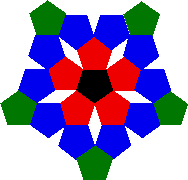
To convert this into an iterated function system, image starting with the initial polygon and scaling by the same factor r = 0.382 used for the Sierpinski pentagon. This time, however, translate six copies so that they would fit exactly inside the initial polygon. The copy in the middle must first be rotated by 180°. Now repeat the construction on each of the six polygons to get the second iteration. Continue indefinitely.
 first iteration |
 second iteration |
 third iteration |
 fourth iteration |
\[\begin{align} {f_1}({\bf{x}}) &= \left[ {\begin{array}{*{20}{c}} {0.382} & 0 \\ 0 & {0.382} \\ \end{array}} \right]{\bf{x}} \\ {f_2}({\bf{x}}) &= \left[ {\begin{array}{*{20}{c}} {0.382} & 0 \\ 0 & {0.382} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {0.618} \\ 0 \\ \end{array}} \right] \\ {f_3}({\bf{x}}) &= \left[ {\begin{array}{*{20}{c}} {0.382} & 0 \\ 0 & {0.382} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {0.809} \\ {0.588} \\ \end{array}} \right] \\ {f_4}({\bf{x}}) &= \left[ {\begin{array}{*{20}{c}} {0.382} & 0 \\ 0 & {0.382} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {0.309} \\ {0.951} \\ \end{array}} \right] \\ {f_5}({\bf{x}}) &= \left[ {\begin{array}{*{20}{c}} {0.382} & 0 \\ 0 & {0.382} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} { - 0.191} \\ {0.588} \\ \end{array}} \right] \\ {f_6}({\bf{x}}) &= \left[ {\begin{array}{*{20}{c}} {-0.382} & 0 \\ 0 & {-0.382} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} { 0.691} \\ {0.951} \\ \end{array}} \right] \\ \end{align}\]
Details are the same as for the Sierpinski pentagon.
\[\sum\limits_{k = 1}^6 {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/6)}}{{\log (r)}} = \frac{{\log (6)}}{{\log (2/(3 - \sqrt 5 )}} = 1.86172\]