Computation of $r$ and $A$ using Geometry and Trigonometry
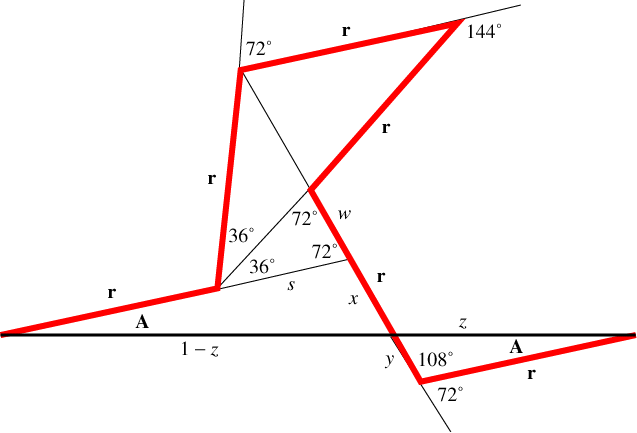
From the isosceles triangle with base $s$, we get that
\[s = 2r\cos {72^ \circ } = r \cdot \frac{{\sqrt 5 - 1}}{2}\]
Combining this result with the two similar triangles involving the angle $A$, we have
\[\frac{r}{z} = \frac{{r + s}}{{1 - z}} = r \cdot \frac{{1 + \sqrt 5 }}{{2(1 - z)}} \quad \Rightarrow \quad z = \frac{{3 - \sqrt 5 }}{2}\]
Next observe that
- \(w = 2s\cos {72^ \circ } = 4r{(\cos {72^ \circ })^2} = r \cdot {\left( {\dfrac{{\sqrt 5 - 1}}{2}} \right)^2} = r \cdot \dfrac{{3 - \sqrt 5 }}{2}\)
- \(\dfrac{y}{r} = \dfrac{x}{{r + s}} \quad \Rightarrow \quad x = y \cdot \dfrac{{r + s}}{r} = y \cdot \dfrac{{\sqrt 5 + 1}}{2}\)
- \(y = r - w - x = r - r \cdot \dfrac{{3 - \sqrt 5 }}{2} - y \cdot \dfrac{{\sqrt 5 + 1}}{2} = r \cdot \dfrac{{\sqrt 5 - 1}}{2} - y \cdot \dfrac{{\sqrt 5 + 1}}{2}\)
\( \Rightarrow \quad y = r \cdot \dfrac{{\sqrt 5 - 1}}{{\sqrt 5 + 3}} = r \cdot \left( {\sqrt 5 - 2} \right)\)
Now use the Law of Cosines on the triangle in the lower right of the figure to solve for $r$:
\[\begin{aligned} {z^2} &= {y^2} + {r^2} - 2yr\cos {108^ \circ } \\ \\ {\left( {\frac{{3 - \sqrt 5 }}{2}} \right)^2} &= {r^2} \cdot {\left( {\sqrt 5 - 2} \right)^2} + {r^2} - 2{r^2} \cdot \left( {\sqrt 5 - 2} \right) \cdot \frac{{1 - \sqrt 5 }}{4} \\ \\ \frac{{7 - 3\sqrt 5 }}{2} &= {r^2} \cdot \frac{{27 - 11\sqrt 5 }}{2} \\ \\ {r^2} &= \frac{{7 - 3\sqrt 5 }}{{27 - 11\sqrt 5 }} = \frac{{6 - \sqrt 5 }}{{31}} \\ \\ r &= \sqrt {\frac{{6 - \sqrt 5 }}{{31}}} \approx 0.34845 \\ \end{aligned}\]
Finally, the Law of Sines on this same triangle allows us to determine the angle $A$:
\[\begin{aligned} \frac{{\sin A}}{y} &= \frac{{\sin {{108}^ \circ }}}{z} \\ \\ \sin A &= \frac{y}{z} \cdot \sqrt {\frac{{5 + \sqrt 5 }}{8}} = r \cdot \frac{{2\left( {\sqrt 5 - 2} \right)}}{{3 - \sqrt 5 }} \cdot \sqrt {\frac{{5 + \sqrt 5 }}{8}} \\ \\ \sin A &= \frac{{\sqrt 5 - 2}}{{3 - \sqrt 5 }} \cdot 2 \cdot \sqrt {\frac{{6 - \sqrt 5 }}{{31}}} \cdot \sqrt {\frac{{5 + \sqrt 5 }}{8}} = \frac{{\sqrt 5 - 1}}{2} \cdot \sqrt {\frac{{25 + \sqrt 5 }}{{62}}} \\ \\ A &= {\sin ^{ - 1}}\left( {\frac{{\sqrt 5 - 1}}{4} \cdot \sqrt {\frac{{25 + \sqrt 5 }}{{62}}} } \right) \approx {11.81858573^ \circ } \\ \end{aligned}\]
Whew, now how's that for an application of geometry and trigonometry!
