Calculation using Complex numbers and Vectors
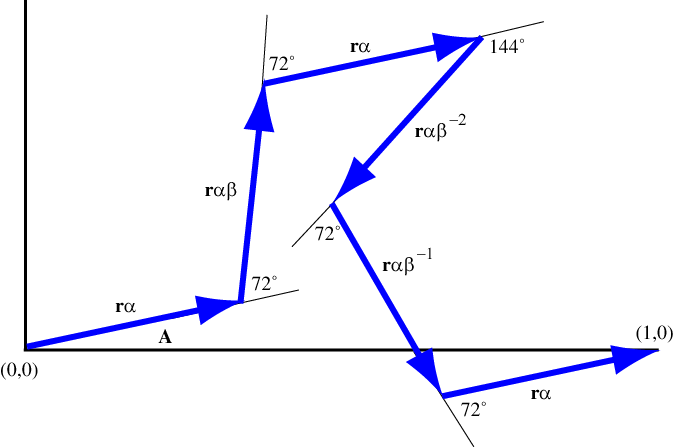
Let \(\alpha = e^{A i}\) (a complex number representing a counterclockwise rotation by $A$ degrees) and \(\beta = {e^{{72^ \circ}i}}\) (a complex number representing counterclockwise rotation by 72 degrees). The first segment can then be represented by the vector \(r\alpha \). Representing the other segments as vectors with the appropriate rotation, we can add the vectors to get a sum that must equal 1, that is
\[\begin{array}{l} r\alpha + r\alpha \beta + r\alpha + r\alpha {\beta ^{ - 2}} + r\alpha {\beta ^{ - 1}} + r\alpha = 1 \\ \\ \Rightarrow r\alpha \left( {3 + \beta + {\beta ^{ - 2}} + {\beta ^{ - 1}}} \right) = 1 \\ \\ \Rightarrow r{e^{Ai}} = \dfrac{1}{{3 + \beta + {\beta ^{ - 2}} + {\beta ^{ - 1}}}} \\ \end{array}\]
Evaluating this complex fraction numerically gives
\[r{e^{Ai}} = \frac{1}{{3 + \beta + {\beta ^{ - 2}} + {\beta ^{ - 1}}}} = 0.34844966{e^{{{11.81858573}^ \circ }i}}\]
This shows that $r$ = 0.34845 and $A$ = 11.81858573°.
To compute the exact value of $r$, we must be more careful with the calculation. Using DeMoivre's Theorem, we first get that
\[\begin{aligned} 3 + \beta + {\beta ^{ - 2}} + {\beta ^{ - 1}} &= 3 + \left( {\cos {{72}^ \circ } + i\sin {{72}^ \circ }} \right) + \left( {\cos ( - {{144}^ \circ }) + i\sin ( - {{144}^ \circ })} \right) + \left( {\cos ( - {{72}^ \circ }) + i\sin ( - {{72}^ \circ })} \right) \\ \\ &= \left( {3 + 2\cos {{72}^ \circ } + \cos {{144}^ \circ }} \right) - i\sin {144^ \circ } \\ \\ &= \left( {3 + 2\cos {{72}^ \circ } - \cos {{36}^ \circ }} \right) - i\sin {36^ \circ } \\ \\ &= \left( {3 + \frac{{\sqrt 5 - 1}}{2} - \frac{{1 + \sqrt 5 }}{4}} \right) - i \cdot \sqrt {\frac{{5 - \sqrt 5 }}{8}} \\ \\ &= \frac{{9 + \sqrt 5 }}{4} - i \cdot \frac{{\sqrt {10 - 2\sqrt 5 } }}{4} \end{aligned}\]
Now taking the reciprocal yields
\[r{e^{{A }i}} = \frac{1}{{\frac{{9 + \sqrt 5 }}{4} - i \cdot \frac{{\sqrt {10 - 2\sqrt 5 } }}{4}}} = \frac{{9 + \sqrt 5 }}{{4\left( {6 + \sqrt 5 } \right)}} + i \cdot \frac{{\sqrt {10 - 2\sqrt 5 } }}{{4\left( {6 + \sqrt 5 } \right)}}\]
The absolute value of this complex number shows us that
\[r = \frac{1}{{\sqrt {6 + \sqrt 5 } }} = \sqrt {\frac{{6 - \sqrt 5 }}{{31}}} \]
There is really no advantage in trying to find an exact value for the angle $A$. But.....if you really need to know, see the derivation using geometry and trigonometry.
