Koch Snowflake IFS Details
IFS
Animation
(hexagons)
This particular IFS is motivated by the following diagram
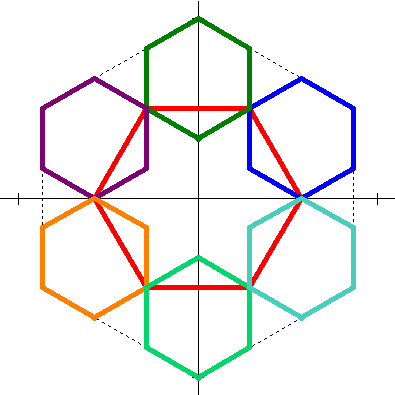
Start with a regular hexagon inscribed in a unit circle (shown by the dotted lines). Six scaled copies of this hexagon can fit inside the original hexagon when scaled by 1/3. Using the six points where these smaller hexagons touch, construct another hexagon (shown in red). The sides of the red hexagon have length equal to \(\sqrt 3\) times the length of the sides of the smaller hexagons, that is, each side of the red hexagon has length \(\sqrt 3 \cdot (1/3) = 1/ \sqrt 3\). Thus the red hexagon has been scaled by \(1/ \sqrt 3\) and rotated by 30°.
Because the affine transformations for the 6 smaller hexagons involve only scaling by 1/3 and translations, each vertex of the initial hexagon is a fixed point for the transformation that translates the scaled version back to that vertex. If we look at a particular vertex $V$ for the corresponding transformation $f(\mathbf{x}) = (1/3)\mathbf{x} + b$, then
\[V = f(V) = \frac{1}{3} V + b \quad \Rightarrow \quad b = \frac{2}{3} V\]
Starting with the vertex in the first quadrant, the vertices are located at the points \(\left( {\cos ({{30}^ \circ } + {{60}^ \circ }k),\sin ({{30}^ \circ } + {{60}^ \circ }k)} \right)\) for $k$ = 0, 1, 2, 3, 4, 5. So the translation for the blue hexagon, for example, is
\[b = \frac{2}{3}\left[ {\begin{array}{cc} {\cos {{30}^ \circ }} \\ {\sin {{30}^ \circ }} \\ \end{array}} \right] = \frac{2}{3}\left[ {\begin{array}{c} {\sqrt 3 /2} \\ {1/2} \\ \end{array}} \right] = \left[ {\begin{array}{c} {1/\sqrt 3 } \\ {1/3} \\ \end{array}} \right]\]
The other translations can be found in a similar way. The red hexagon does not need to be translated once scaled and rotated.
Notice that the outside boundary formed by the six smaller hexagons in this IFS construction consists of six copies of the first iteration in the construction of Koch curves, as illustrated in the image on the left using just one side of the initial hexagon. The second iteration of the IFS will construct the second iteration of a Koch curve along each side of the initial hexagon, as shown in the image on the right.
Convergence
Demonstration
Video
This will continue with each subsequent iteration of the IFS also constructing iterates of the Koch curves along the boundary. Thus in the limit, this iterated function system will not only produce the Koch snowflake, but the boundary of the snowflake will consist of copies of the Koch curves along the six sides of the original hexagon, with each Koch curve pointed into the hexagon. This provides an alternative method of constructing the snowflake via Koch curves from the sides of a hexagon, and is an important tool in tiling the plane with copies of Koch snowflakes [Tiling Details].
Why is the Koch snowflake the attractor for this IFS?
The Koch snowflake is constructed by starting with an equilateral triangle and adding scaled copies around the edges. The sets $S_n$ that come from iterating this construction $n$ times form a Cauchy sequence in the Hausdorff metric and the limit is the Koch snowflake.
Let $H_n$ be the set obtained from applying $n$ iterations of the IFS described above to the initial set $H_0$ that is a filled regular hexagon as shown in the left figure below (this corresponds to the hexagon used in describing the IFS above). An equilateral triangle representing $S_0$ in the construction of the Koch snowflake can be inscribed in this hexagon as shown in the figure to the right.
Applying the IFS to the hexagon to get $H_1$ and applying the first iteration for the Koch snowflake to get $S_1$ yields the following images which show again how $S_1$ fits exactly inside $H_1$.
Continuing the iteration of both the IFS and the Koch snowflake construction shows that $S_n$ will fit inside $H_n$ and suggests that the two images will merge in the limit as $n$ goes to infinity.
That each $S_n$ is a subset of $H_n$ for all n can be confirmed by induction. The image above shows that it is true for $n$ = 0. Assume that $S_k$ is a subset of $H_k$, and that each side of $S_k$ forms an isosceles triangle with the base being a side of $S_k$ and the other two sides being sides of $H_k$ as shown in the image below. We want to show that the same thing occurs for iteration $k+1$.
If the side of $H_k$ has length \(a\), then the base of the isosceles triangle has length \(a\sqrt{3}\) and the height of the isosceles triangle is \[\displaystyle a\cdot\sin(30^\circ) = \frac{a}{2}.\] Now in forming $S_{k+1}$, the base of the isosceles triangle extends outward to form an equilateral triangle as shown in the next image.
The sides of this equilateral triangle have length \(\displaystyle \frac{a\sqrt{3}}{3}\) and therefore the height of the equilateral triangle is \[\displaystyle \frac{a\sqrt{3}}{3}\cdot \sin(60^\circ) = \frac{a\sqrt{3}}{3}\cdot\frac{\sqrt{3}}{2} = \frac{a}{2}.\] This is the same height as the original isosceles triangle, which shows that the construction of $S_{k+1}$ has split the original $H_k$ region into two smaller isosceles triangles each of whose base is a side of $H_k$. Now the same argument shows that in the construction $H_{k+1}$, the part of the Koch curve drawn inside $H_k$ will create two smaller isosceles triangles that have a base that is a side of $S_{k+1}$.
This shows that the new parts of $S_{k+1}$ lie inside the new parts of $H_{k+1}$, and that each side of $S_{k+1}$ forms an isosceles triangle with the base being a side of $S_{k+1}$ and the other two sides being sides of $H_{k+1}$. By induction, those properties are true for all $n$.
The Hausdorff distance between two compact sets $A$ and $B$ is given by
\[D(A,B) = \inf \left\{ {r:A \subseteq {N_r}(B) \text{ and } B \subseteq {N_r}(A)} \right\}\]
where for a set $W$, $N_r(W)$ is the $r$-envelope of $W$; that is, the set of all points that are within a distance $r$ of some point in $W$.
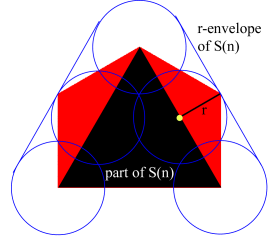Let $s$ be the length
of the sides of the equilateral triangle in $S_0$.
Because $S_n$ is a subset of $H_n$, then $S_n$ is also a
subset of the $r$-envelope of $H_n$ for all values of
$r$. Therefore we only need to look at the values of $r$
for which $H_n$ is a subset of the $r$-envelope of
$S_n$. The figure to the right indicates that the smallest such $r$ value is given by the height of the isosceles triangles from that part of each small scaled hexagon that extends outside the scaled triangles in the Koch construction for $S_n$. Because these hexagons and triangles are scaled by 1/3 at each iteration,
the distance between the two sets $H_n$ and $S_n$ is therefore given by \[d(H(n),S(n)) = \frac{s}{{2\sqrt 3 }} \cdot {\left( {\frac{1}{3}} \right)^n}\] We see that the distance goes to 0 in the limit as $n$ goes to infinity. Since the sets $S_n$ converge to the Koch snowflake in this metric, this means that the sets $H_n$ will also converge to the Koch snowflake. Hence the Koch snowflake is the attractor for this iterated function system.
