Heighway Dragon Components

Central
Component

Ngai and Nguyen [2003] showed that the Heighway dragon is a countable union of closed geometrically similar disk-like planar sets, any two of which intersect at no more than one cut point. The following figure shows the largest (central) component of the dragon in red.

The red component consists of two copies of the dragon scaled by $\sqrt{2}/4$, one rotated by 45° clockwise and the other rotated by 135° counterclockwise, one copy of the central component scaled by 1/2 and rotated by 180°, and two copies of the central component scaled by 1/4. The two copies of the dragon form a twindragon.

a scaled copy of the dragon rotated by 45 degrees a copy of the central component scaled by 1/2 a second copy of the central component scaled by 1/4

You can add the pieces to the central component by clicking on the buttons to the left in sequence.

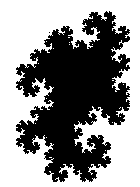
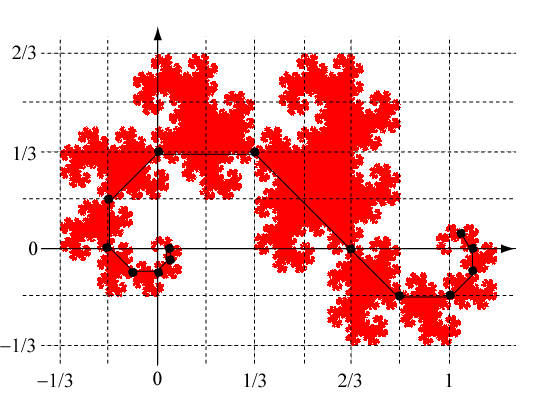
Cut points

The cut points are where each component touches the components on either side. Click the button on the left to show some of the cut points on the Heighway dragon as shown below for which the initial segment in the construction lies along the x-axis from $x = 0$ to $x = 1$. These cut points lie on two logarithmic spirals that pass through the dragon. Click the button to add these spirals to the figure.

Proofs

The cut points for the components to the left of the central component are located at \[\begin{array}{l} x_L(n) = \frac{\sqrt{2}}{3}\,2^{-n/2} \, \cos \left( (n + 1)\frac{\pi}{4} \right) \\ y_L(n) = \frac{\sqrt{2}}{3}\,2^{-n/2}\, \sin \left( (n + 1) \frac{\pi}{4} \right) \\ \end{array}\] for n ≥ 0. For the points in the figure, these are (1/3, 1/3), (0, 1/3), (-1/6, 1/6), (-1/6, 0), (-1/12, -1/12), (0, -1/12), (1/24, -1/24), (1/24, 0), (1/48, 1/48), and (0,1/48).

The cut points for the components to the right of the central component are located at \[\begin{array}{l} x_R(n) = 1 - \frac{\sqrt{2}}{3}\,2^{-n/2} \, \sin \left( (n + 1)\frac{\pi}{4} \right) \\ y_R(n) = \frac{\sqrt{2}}{3}\,2^{-n/2} \, \cos \left( (n + 1)\frac{\pi}{4} \right) \\ \end{array}\] for $n \ge 1$. For the points in the figure, these are (2/3, 0), (5/6, -1/6), (1, -1/6), (13/12, -1/12), (13/12, 0), (25/24, 1/24), (1,1/24) ,(47/48, 1/48), and (47/48, 0).

You can get a sense of why these cut points arise and where by looking at the 10th iteration of the Heighway dragon starting with the unit line segment from (0,0) to (1,0). In the figure below, where the iteration is superimposed on top of the dragon, the places where the segments do not enclose a complete square are the locations where the cut points will arise in the limit as the number of iterations goes to infinity.

[Enlarge]

Other
Components

Component
Animation

The figures above and the formulas for the cut points suggest that starting with the central component, the other components can be obtained by scaling each component by $1/\sqrt 2$ and rotating by 45° to get the next component in the spiral towards either (0,0) or (1,0). This is what actually happens. The one exception is that starting with the central component, the first component to the right is a copy of the central component scaled by 1/2 and rotated 180° (this can be seen in the figure showing the cut points). Other than this, this first component on the right is the same as the second component to the left. Indeed all the components to the right of the central component are a copy of the corresponding components on the left excluding the first left component. So these components on the left and right are geometrically similar to the central component. Therefore each component can also be decomposed into a twindragon, a copy of the component scaled by 1/2 and rotated by 180°, and two copies of the component scaled by 1/4.

Each component of the dragon shown in a different color.

The figures below show how the components continue to repeat as you zoom in (going from left to right, as indicated by the square boxes). Click on each image for a larger view.

Component
Areas

Let $C_0$ represent the central component and let $A$ be the area of this component. Label the components to the left as $C_k$ for $k$ from 1 to infinity. Because $C_k$ is obtained from $C_0$ by a scaling by $\left( 1/ \sqrt 2 \right)^k$, the area of $C_k$ is equal to ${\left( {1/2} \right)^k}A$. Each component to the right of the central component has the same area as the corresponding component to the left starting with $k$ = 2. The total area, $H$, of the Heighway dragon is therefore \[H = A + \frac{1}{2}A + 2\left( {\frac{1}{4}A + \frac{1}{8}A + \ldots } \right) = A + \frac{1}{2}A + A = \frac{5}{2}A\]

Hence $A = (2/5)H$. The areas of the other components can be found by dividing by an appropriate power of 2.

We know that the central component of the Heighway dragon consists of 2 copies of the dragon, each scaled by $\sqrt{2}/4$, one copy of the central component scaled by 1/2, and two copies of the central component scaled by 1/4. Taking the sum of the areas of these 5 pieces shows that

\[2\left( {\frac{1}{{8}}H} \right) + \frac{1}{4}A + 2\left( {\frac{1}{{16}}} \right)A = 2\left( {\frac{5}{{16}}A} \right) + \frac{1}{4}A + \frac{1}{8}A = \frac{5}{8}A + \frac{1}{4}A + \frac{1}{8}A = A\]

Therefore the five parts of the central component must be essentially disjoint.

Classic Iterated Function Systems