File Menu

New/IFS (F5)
New/Chaos Game (F6)
New/Sierpinski Triangle Game (F9)
New/Fractal Transformation Movie (F11)
New/Deterministic Fractal Movie (F12)

Choose New/IFS to get the traditional view of an iterated function system given in terms of an affine transformation of the form f(x) = Ax+b, where A is a 2x2 matrix and b is a translation vector (this is the IFS mode.) The default transformation is an IFS that scales by a factor of 1/2.

Choose New/Chaos Game to design an iterated function system based on the rules of the "chaos game" (this is the Chaos Game mode.) In this view you choose the location of your fixed points, then describe the moves of a point with respect to each fixed point. These moves consist of scaling towards the fixed point, rotation with respect to the fixed point, or a horizontal or vertical reflection across a line through the fixed point.

The Sierpinski Triangle Game is based on The Chaos Game, a java applet created by Johanna Voolich and Robert Devaney at http://math.bu.edu/DYSYS/applets/chaos-game.html. You will be presented initially with the second iteration of the Sierpinski Triangle. This consists of nine subtriangles, one of which is colored red. This is the target triangle. You will also see a blue dot at one of the three corners of the large triangle. The goal of the game is to move the blue dot into the interior of the red target triangle (so not just on the boundary, but actually inside the triangle.) Other versions of the game allow for one or three rotations with the Sierpinski Triangle iterated functions. See the individual help file for the game (also available from the Help menu when the game is started).

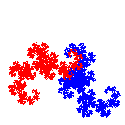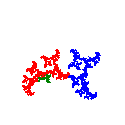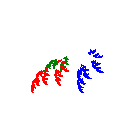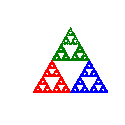
fractal movie

Choose New/Fractal Transformation Movie to open the fractal movie creator for constructing a sequence of movie frames that evolve from the fractal for an initial IFS (first frame) to the fractal for a final IFS (last frame). The transformation from one fractal to the other is done either by a linear interpolation between the affine maps in each IFS, or between the scaling and rotation values corresponding to the affine maps in each IFS. If the same IFS is chosen for both the initial and final frames, then the transformation is obtained by selecting one of the maps in that IFS and rotating that map through 360 degrees while keeping the other maps unchanged. See the individual help file for more details (also available from the Help menu for the fractal movie creator.

Choose New/Deterministic Fractal Movie to open a dialog box when using the deterministic algorithm to construct a sequence of movie frames that step through a sequence of iterations. This is saved to a file as an animated gif and can be viewed in the Fractal Movie Viewer. See the individual help file for more details.

Open IFS File/Open Chaos Game File (Ctrl-O)
Append IFS File/Append Chaos Game File

Choose Open to load the IFS definitions from a file. If you are in the Chaos Game mode, then the Open command will load the chaos game moves from a file. This will create a new list of fractals in the Fractals menu. Choose Append to append the IFS definitions or chaos game moves in a file to the current list of fractals. There is a maximum of 30 fractals that can be listed in the Fractals menu. Anything above 30 in an IFS file or a Chaos Game file will be ignored, and you can only append new items until the list has a total of 30 items.

IFS files are text files using the same format as for the program Fractint. Each IFS is described using the following syntax: 

Heighway {; Heighway Dragon                                                     
; Edgar, "Measure, Topology, and Fractal Geometry"                    
; Page 19                                                            
   0.5 -0.5  0.5  0.5  0  0  0.5 
  -0.5 -0.5  0.5 -0.5  1  0  0.5 
}
The first line contains the name of the fractal followed by an opening bracket {. Anything after a semi-colon is treated as a comment and ignored (although comments can be displayed from within IFS Exploration.) There can be up to 20 lines of comments, each of length less than 70 characters.

Following the comments (if any) are lines representing each function in the IFS. There should be 6 or 7 numbers on each line. The first four are the entries of the matrix A. The next two are the entries of the translation vector. If there is a 7th number on the line, it will represent a probability. The numbers in each line should be separated by spaces, tabs, or commas. There can be at most 100 functions in each IFS.

A closing bracket } on its own line will indicate the end of the IFS definition.

A file should contain at most 30 different iterated function systems.

Chaos game files are text files that have the extension ".chg". Here is an example of a file with the code the chaos game moves for the Sierpinski Triangle. 
Sierpinski Triangle { "Chaos Rules"
;Math Horizons, Nov. 2004
;Bob Devaney
  S  0.500000  0.000000  0.333333  0.000000  0.000000 
  S  0.500000  0.000000  0.333333  1.000000  0.000000 
  S  0.500000  0.000000  0.333333  0.500000  0.866025 
}

The first line contains the name of the fractal followed by an opening bracket {. Following the comments (if any) are lines representing the chaos game moves. There should be 6 items on each line. The first is a string containing the four possible moves (S-scaling, R-rotation, H-horizontal reflection, and V-vertical reflection). Following this are the scaling factor, the rotation angle, the probability, and the coordinates of the fixed point. The numbers in each line should be separated by spaces, tabs, or commas.

Open Fractal Movie...

This will open a fractal movie (see above) saved as an animated gif in the Fractal Movie Viewer. The viewer can play the movie once or loop continuously. You can change the speed at which the movie is played, and step forward or backward through each frame.

Open Recent

The 6 most recent IFS or CHG files that have been opened will be listed here, in chronological order. This list is saved in the ifskit.ini file. You can clear the list with the menu item "Clear List". If you try to open a file that can no longer be found, you will have the option to remove that file from the list.

Save IFS Fractals List/Save Chaos Game Fractals List
Save IFS Fractals List As/Same Chaos Game Fractals List As
Save Current IFS to File/Save Current Chaos Game to File

The first two items will save the list of iterated function systems in the Fractals menu to a text file. The last item will save only the current IFS to a file. If you are in the Chaos Game mode, only the chaos game moves will be saved to the file.

Save Fractal Picture
Save Design Picture

These two items will save either the picture in the Fractal window or the picture in the Design window in jpg, gif, png, or bitmap format.
Important Note: Saving images in jpg, gif, or png format requires that FreeImage.dll exist either in the same folder as the IFS Construction Kit program or in the windows/system folder. FreeImage.dll is included in the zip file for IFS Construction Kit that can be downloaded from https://larryriddle.agnesscott.org/ifskit.

Save Initial Polygon

This will save the initial polygon used in the Design window to a text file as a list of coordinates.

Print

The Print dialog box allows you to print the images in the fractal and design windows, the IFS code in matrix and scale/rotation form, and the chaos game rules. There are several options available for adjusting the layout of the printed items.

While you can choose which printer to use, you will not have access to a separate dialog box that handles the preferences for that printer. In addition, there is no way to change the format of the text. If you need more control over the format, you can print the IFS code to a text file which you can then open in Notepad, Wordpad, or Microsoft Word. You can copy and paste the images in the fractal and design windows into Word if necessary.