



The following table shows the result of combining one transformation with another. The one down the rows is done first, followed by the one across the columns. If we call the transformations gn for n = 1, 2, 3, 4, 5, 6, 7, 8 then the table shows the result of the composition \(g_c \circ g_r\), where r and c denote row and column.
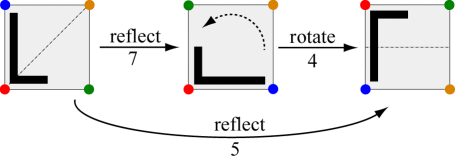
\[\begin{array}{*{20}{c}} {} & {\begin{array}{*{20}{c}} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \end{array} } \\ {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \\ 8 \\ \end{array} } & {\boxed{\begin{array}{*{20}{c}} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 3 & 4 & 1 & 8 & 7 & 5 & 6\\ 3 & 4 & 1 & 2 & 6 & 5 & 8 & 7\\ 4 & 1 & 2 & 3 & 7 & 8 & 6 & 5\\ 5 & 7 & 6 & 8 & 1 & 3 & 2 & 4\\ 6 & 8 & 5 & 7 & 3 & 1 & 4 & 2\\ 7 & 6 & 8 & 5 & 4 & 2 & 1 & 3\\ 8 & 5 & 7 & 6 & 2 & 4 & 3 & 1\\ \end{array} }} \\ \end{array} \]So, for example, applying a reflection across the lower left to upper right diagonal (#7) followed by a rotation by 270° (#4) is the same as doing a vertical reflection (#5), as illustrated below. Hence \(g_5 = g_4 \circ g_7\).
Suppose we compose the elements of D4 with the k functions \(\{h_i\}\) in an IFS. The new IFS would consists of 8k functions, and its unique attractor B would satisfy $$ B = \bigcup_{i=1}^k \Big( g_1 \circ h_i(B) + g_2 \circ h_i(B) + g_3 \circ h_i(B) + g_4 \circ h_i(B) + g_5(B) \circ h_i(B) \\ \qquad+ g_6(B) \circ h_i + g_7 \circ h_i(B) + g_8 \circ h_i(B) \Big) $$
Now if we apply the \(g_7\) reflection to the set B, we would get
\( g_7(B) = \displaystyle\bigcup_{i=1}^k \Big( g_7 \circ g_1 \circ h_i(B) + g_7 \circ g_2 \circ h_i(B) +g_7 \circ g_3 \circ h_i(B) +g_7 \circ g_4 \circ h_i(B) + g_7 \circ g_5(B) \circ h_i(B) \\ \qquad\qquad\qquad+ g_7 \circ g_6(B) \circ h_i +g_7 \circ g_7 \circ h_i(B) +g_7 \circ g_8 \circ h_i(B) \Big) \\ \qquad= \displaystyle\bigcup_{i=1}^k \Big( g_7 \circ h_i(B) + g_5 \circ h_i(B) + g_8 \circ h_i(B) + g_6 \circ h_i(B) + g_2(B) \circ h_i(B) \\ \qquad\qquad\qquad+ g_4(B) \circ h_i + g_1 \circ h_i(B) + g_3 \circ h_i(B) \Big) \\ \qquad = B \)
This shows that B is symmetric with respect to that reflection. A similar calculation would show that \(g_i(B) = B\) for all 8 elements in D4, and thus B would be symmetric with respect to each of those rotations and reflections.