Sierpinski Pedal Triangle

Let T = S(0) be an acute triangle with vertices A, B, and C. The pedal triangle of T is the triangle formed by the three points A1, B1, and C1 that lie at the feet of the three altitudes of T, i.e. from each vertex drop a perpendicular to the opposite side until it intersects with that side.

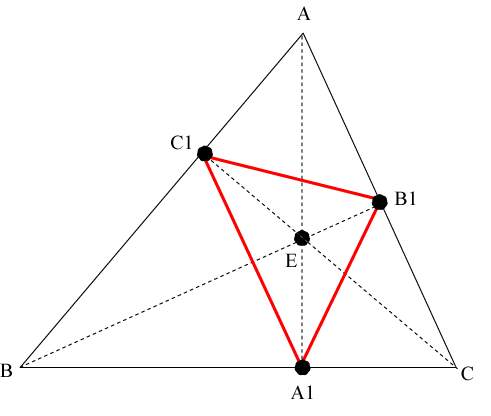
The point E where there three altitudes intersect is the orthocenter of triangle T. The pedal triangle divides the original triangle into four smaller triangles. Remove the interior of the pedal triangle to get S(1).

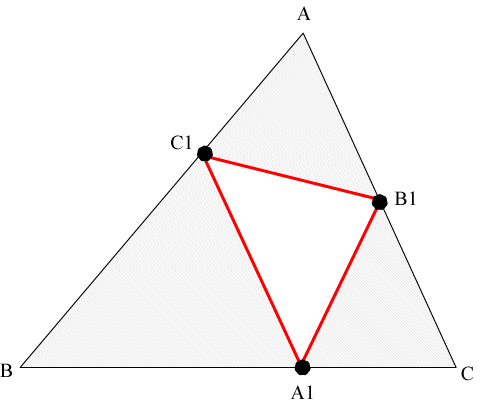
Each of the three remaining triangles is similar to the original triangle T [Proof]. Now repeat this procedure and remove the pedal triangle for each of these three remaining triangles to obtainS(2).

S(0)	S(1)
S(2)	S(3)

Continue to repeat the construction to obtain a decreasing sequence of sets

$$ S(0) \supset S(1) \supset S(2) \supset S(3) \supset \cdots $$

The Sierpinski pedal triangle is the intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often. When the triangle is equilateral, the construction just produces the usual Sierpinski triangle. This generalization of the Sierpinski triangle was first studied in 2008 by Xin-Min Zhang, Richard Hitt, Bin Wang, and Jiu Ding [1].

The three triangles left after the pedal triangle is removed can be obtained from the original triangle by a sequence of scaling, reflection, rotation, and translation. We will take vertex B to be the origin and vertex C to be at the point (1,0) on the x-axis. The transformations are then completely determined by the three angles of the original triangle.

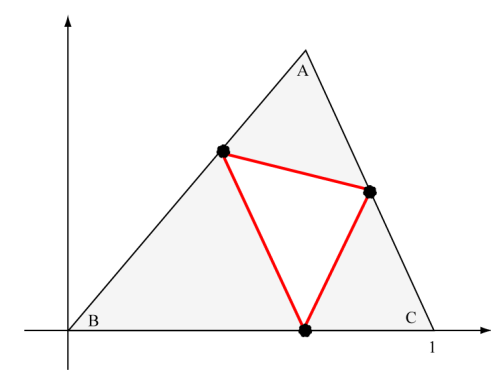
If we let A, B, and C represent the angles in the figure above, then the IFS is given by the following three functions [Proof].

\({f_B}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {{{\cos }^2}(B)} & {\cos (B)\sin (B)} \\ {\cos (B)\sin (B)} & { - {{\cos }^2}(B)} \\ \end{array}} \right]{\bf{x}}\)	scale by cos(B) vertical reflection rotate by B
\({f_C}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} {{{\cos }^2}(C)} & { - \cos (C)\sin (C)} \\ { - \cos (C)\sin (C)} & { - {{\cos }^2}(C)} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {{{\sin }^2}(C)} \\ {\cos (C)\sin (C)} \\ \end{array}} \right]\)	scale by cos(C) vertical reflection rotate by −C
\({f_A}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}} { - \cos (A)\cos (C - B)} & {\cos (A)\sin (C - B)} \\ {\cos (A)\sin (C - B)} & {\cos (A)\cos (C - B)} \\ \end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}} {{{\sin }^2}(C)} \\ {\cos (C)\sin (C)} \\ \end{array}} \right]\)	scale by cos(A) horizontal reflection rotate by −(C−B)

Note: If vertex C is at some other point on the x-axis, then the translation vectors should be multiplied by the length of the segment BC.

The following video shows an animation that summarizes the steps in the iterated function system for generating a Sierpinski pedal triangle.

The Sierpinski Pedal Triangle consists of three self-similar pieces corresponding to the three functions in the iterated function system.

70°-60°-50° Sierpinski Pedal Triangle
[Enlarge]

The Sierpinski pedal triangle is self-similar with 3 non-overlapping copies of itself, each scaled by the factors cos(A), cos(B), and cos(C), respectively. Therefore the similarity dimension, d, of the attractor of the IFS is the solution to the Moran equation \[\cos {(A)^d} + \cos {(B)^d} + \cos {(C)^d} = 1\]

If all three angles are positive, then the derivative of the function \(h(d) = \cos {(A)^d} + \cos {(B)^d} + \cos {(C)^d}\) is \[h'(d) = \ln(\cos A) \cos {(A)^d} + \ln(\cos B)\cos {(B)^d} + \ln(\cos C)\cos {(C)^d}\] which is negative for all \(d >0\) since all the cosine values are less than 1. Since h(0)=3 and \(h\) is strictly decreasing to 0 as d increases, there is a unique solution to \(h(d)=1\). If one of the angles is 90°, say angle \(A\), then the initial triangle is a right triangle and the equation reduces to \(\cos {(B)^d} + \cos {(C)^d} = 1\) where \(B+C = 90^\circ\). Then the unique solution is \(d = 2\) since \[\cos {(B)^2} + \cos {(C)^2} = \cos {(B)^2} + \cos{(90^\circ-B)}^2 = \cos {(B)^2} + \sin {(B)^2} = 1\]

The 65°-50°-65° Sierpinski pedal triangle shown above has dimension 1.59572.

The 70°-60°-60° Sierpinski pedal triangle has dimension 1.60410.

The figures below show a 30°-75°-75° Sierpinski pedal triangle with dimension 1.65931 and a 55°-85°-40° triangle with dimension 1.79750. Ding and Li [2] proved that the ordinary Sierpinski gasket (where all angles equal 60°) has the smallest fractal dimension among all Sierpinski pedal triangles.

 

Notice that as the original triangle ΔABC approaches a right triangle, the dimension of the corresponding Sierpinski pedal triangle approaches the value 2. If, in fact, ΔABC is a right triangle, then the pedal triangle is actually just a line segment that divides ΔABC into two similar right triangles. So there is nothing to "remove" at each step in the iterative construction and the Sierpinski pedal triangle is just the original ΔABC with dimension 2. You can see the "pedal triangle" line segments filling up the original triangle in the animation. The second animation starts with a right triangle and shows the transition in the Sierpinski pedal triangles as the top vertex moves horizontally from the initial right triangle to an isosceles triangle then back to a right triangle.

 

1. Xin-Min Zhang, Richard Hitt, Bin Wang, and Jiu Ding. "Sierpinski Pedal Triangles," Fractals, Vol. 16, No. 2 (2008), 141-150 [Preprint available at http://www.richardhitt.com/research/hittzhang.pdf]
2. Jiu Ding and Zhao Li. "On The Dimension Of Sierpiński Pedal Triangles", Fractals, Vol. 17, No. 1 (2009) 39–43