$$\begin{array}{l} r = {r_k} \cdots {r_2}{r_1}{r_0} = {r_0} + {r_1}p + {r_2}{p^2} + \cdots + {r_k}{p^k} \qquad (0 \le {r_i} \lt p) \\ c = {c_k} \cdots {c_2}{c_1}{c_0} = {c_0} + {c_1}p + {c_2}{p^2} + \cdots + {c_k}{p^k} \qquad (0 \le {c_i} \lt p) \\ \end{array}$$
Then
$$\left( {\begin{array}{*{20}{c}} r \\ c \\ \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{r_0}} \\ {{c_0}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{r_1}} \\ {{c_1}} \\ \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{r_1}} \\ {{c_1}} \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}{c}} {{r_k}} \\ {{c_k}} \\ \end{array}} \right)(\bmod p)$$
We take here the standard convention that the binomial coefficient (r,c)=0 if c > r.
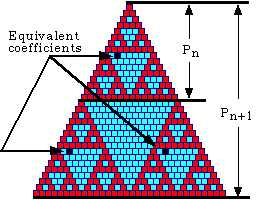
To look at Pascal's triangle (mod 2), take p=2. Let's take a look at the binomial coefficient (r,c) in row r and column c of Pn. Because Pn has only 2n rows, both r and c are less than 2n. Therefore they can be written in binary notation as
$$\begin{array}{l} r = {r_{n-1}} \cdots {r_2}{r_1}{r_0} \qquad (0 \le {r_i} \lt 2) \\ c = {c_{n-1}} \cdots {c_2}{c_1}{c_0} \qquad (0 \le {c_i} \lt 2) \\ \end{array}$$
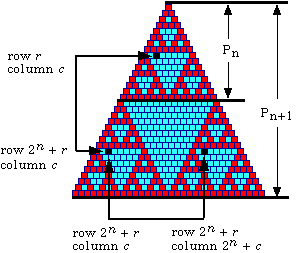Also, since Pn has a total of 2n rows,
and has 2n columns in the last row, the binomial
coefficient in the equivalent position in the lower left triangular corner
of Pn+1 is (2n+r, c) and the binomial coefficient
in the equivalent position in the lower right triangular corner is
(2n+r, 2n+c).
But then by Lucas's Theorem, we have
$$ \begin{align} \left( {\begin{array}{*{20}c} {2^n + r} \\ c \\ \end{array}} \right)\,(\bmod 2) &= \left( {\begin{array}{*{20}c} {1{\kern 1pt} {\kern 1pt} r_{ n - 1} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{ 0} } \\ {0{\kern 1pt} {\kern 1pt} c_{ n - 1} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} c_{ 0} } \\ \end{array}} \right)\,(\bmod 2) = \left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}c} {r_{ 0} } \\ {c_{ 0} } \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} {r_{ n - 1} } \\ {c_{ n - 1} } \\ \end{array}} \right)\;(\bmod 2) \\ &= \left( {\begin{array}{*{20}c} {r_{ 0} } \\ {c_{ 0} } \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} {r_{ n - 1} } \\ {c_{ n - 1} } \\ \end{array}} \right)\;(\bmod 2) = \left( {\begin{array}{*{20}c} r \\ c \\ \end{array}} \right)\,(\bmod 2) \\ \end{align} $$
$$ \begin{align} \left( {\begin{array}{*{20}c} {2^n + r} \\ {2^n + c} \\ \end{array}} \right)\,(\bmod 2) &= \left( {\begin{array}{*{20}c} {1{\kern 1pt} {\kern 1pt} r_{{\kern 1pt} n - 1} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{ 0} } \\ {1{\kern 1pt} {\kern 1pt} c_{ n - 1} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} c_{ 0} } \\ \end{array}} \right)\,(\bmod 2) = \left( {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array}} \right)\left( {\begin{array}{*{20}c} {r_{ 0} } \\ {c_{ 0} } \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} {r_{ n - 1} } \\ {c_{ n - 1} } \\ \end{array}} \right)\;(\bmod 2) \\ &= \left( {\begin{array}{*{20}c} {r_{ 0} } \\ {c_{ 0} } \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} {r_{ n - 1} } \\ {c_{ n - 1} } \\ \end{array}} \right)\;(\bmod 2) = \left( {\begin{array}{*{20}c} r \\ c \\ \end{array}} \right)\,(\bmod 2) \\ \end{align} $$
Therefore all three binomial coefficients have the same value (mod 2) and hence would have the same color in Pascal's triangle (mod 2). This proves the first part of the recursive behavior of Pascal's triangle.
To prove the second part, we must show that the three equivalent corner triangles of Pn+1 surround a triangle of even numbers. Again we appeal to Lucas's Theorem. The last row of Pn corresponds to r = 2n-1. The next row therefore has r = 2n and columns 0 <= c <= 2n. The first and last values in this row are equal to 1. These are the top squares in the lower left and lower right triangular corners, respectively. For all the other columns in the row, however, at least one binary digit in c will be a 1 and therefore for 1 ≤ c ≤ 2n−1
$$ \begin{align} \left( {\begin{array}{*{20}c} {2^n } \\ c \\ \end{array}} \right)\, &= \left( {\begin{array}{*{20}c} {1{\kern 1pt} {\kern 1pt} 0 \cdots {\kern 1pt} {\kern 1pt} 0} \\ {0{\kern 1pt} c_{n - 1} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} c_0 } \\ \end{array}} \right)\, \\ &= \left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array}} \right)\left( {\begin{array}{*{20}c} 0 \\ {c _{n - 1} } \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} 0 \\ {c_0 } \\ \end{array}} \right)\;(\bmod 2) = 0 \\ \end{align} $$
since (0,1) = 0. Hence this row starts and ends with an odd number, but all the remaining numbers are even.
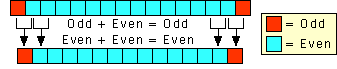What happens in the next row? Recall that
(r+1,c) = (r,c) + (r,c-1). Therefore each number in the next row is the
sum of two adjacent numbers in the current row. But the sum of an odd and
an even number is odd, and the sum of two even numbers is even. Therefore
the string of even numbers produces a new string of even numbers bounded
on both ends by an odd number, with the new string of even numbers
containing one less value than the previous row. Each time we move to the
next row we reduce the string of even numbers by 1. By the time we reach
the last row of Pn+1, we have eliminated all the even numbers.
Thus we have produced the inner triangle of even numbers. The last row
will consist of all odd numbers since for this row r = 2n+1-1
and
$$ \left( {\begin{array}{*{20}c} {2^{n + 1} - 1} \\ c \\ \end{array}} \right)\, = \left( {\begin{array}{*{20}c} {1{\kern 1pt} 1 \cdots 11} \\ {{\kern 1pt} c_n {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} c_0 } \\ \end{array}} \right)\, = \left( {\begin{array}{*{20}c} 1 \\ {c_n } \\ \end{array}} \right) \cdots \left( {\begin{array}{*{20}c} 1 \\ {c_0 } \\ \end{array}} \right)\;(\bmod 2) = 1 $$
For a different proof of why the binary coloring of Pascal's triangle generates the same image as the Sierpinski gasket, watch the YouTube video by Robin Truax called "The Tale of Three Triangles".
