
binomial
coefficient
$$\left( {\begin{array}{*{20}{c}} r \\ c \\ \end{array}} \right) = \frac{{r!}}{{c!\left( {r - c} \right)!}}$$


binomial
 Does the figure to the right
appear to be the Sierpinski gasket? Actually, it
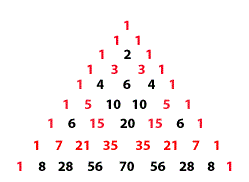
is a representation of Pascal's triangle (mod 2). The first 9 rows of Pascal's
triangle consist of the following
binomial coefficients:
Does the figure to the right
appear to be the Sierpinski gasket? Actually, it
is a representation of Pascal's triangle (mod 2). The first 9 rows of Pascal's
triangle consist of the following
binomial coefficients:
To understand why Pascal's triangle mod 2 resembles the Sierpinski gasket, let Pn denote the first 2n rows of the triangle and consider what happens in going from Pn to Pn+1.
|
Here are the first 8 rows of Pascal's triangle. Notice that it has the identical pattern in each of the three corners which surround a black triangle of even numbers. |
|
Here we see that the three corners of P4 contain identical copies of P3 each scaled by 1/2, surrounding a solid black triangle of even numbers. |
|
Again, the three corners of P5 contain identical copies of P4 each scaled by 1/2, surrounding a solid black triangle of even numbers. |
|
The three corners of P6 contain identical copies of P5 each scaled by 1/2, surrounding a solid black triangle of even numbers. |
The odd binomial coefficients form a discrete variant of the Sierpinski gasket in which the iterative process of going from one stage to the next is the same as with the gasket: make 3 copies, each scaled by 1/2, and translate to the appropriate corner. In the "limit", the Pascal triangle with an infinite number of rows would have the same self-similarity property as the Sierpinski gasket.
Here is a proof of the mathematical justification for this behavior.