
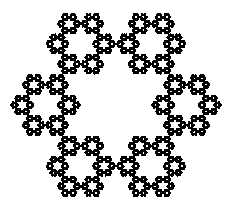
Here is the limit set starting with an octagon (n = 8 and r = 0.292893)

and the limit set starting with a regular polygon with 15 sides (n = 15 and r = 0.172909).



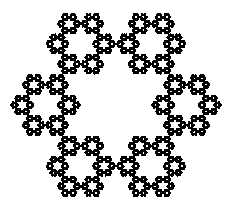
Here is the limit set starting with an octagon (n = 8 and r = 0.292893)

and the limit set starting with a regular polygon with 15 sides (n = 15 and r = 0.172909).

\[r_n = \frac{1}{{2 \; \left( {1 + \sum\limits_{k = 1}^{\left\lfloor {n/4} \right\rfloor } {\cos \left( {\frac{{2\pi k}}{n}} \right)} } \right)}}\]
where \({\left\lfloor {n/4} \right\rfloor }\) denotes the greatest integer less than or equal to n/4. As n increases, the scaling factor \(r_n\) converges to 0 and the Sierpinski n-gons converge to a circle.
The only affine transformations needed for the iterated function system is scaling by \(r_n\) and translations. The translations can be taken to be
\[\left[ {\begin{array}{*{20}{c}} {(1 - r_n)w\cos \left( {\frac{{2\pi k}}{n}} \right)} \\ {(1 - r_n)w\sin \left( {\frac{{2\pi k}}{n}} \right)} \\ \end{array}} \right]\]
for k = 1 to n, where w is the radius of the initial polygon, that is, the distance from the center of the polygon to each vertex.
Click here for the details.
\[\sum\limits_{k = 1}^n {{r^d}} = 1 \quad \Rightarrow \quad d = \frac{{\log (1/n)}}{{\log (r_n)}} \]
Here is a graph of the dimension of the n-gon for n from 3 to 30.
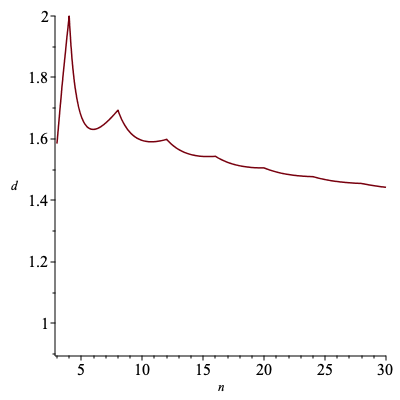
As n goes to infinity, the dimension converges to 1. [Details]
Here is a graph of \(n \cdot r_n^2\) for n from 3 to 16.
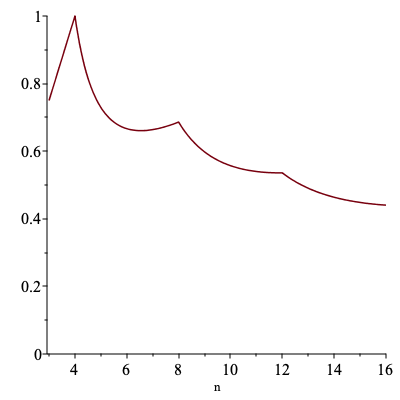
Notice that \(n \cdot r_n^2 \lt 1\) for \(n > 4\). Therefore the area of G(m) will go to 0 as m goes to infinity. This means that we have removed "all" of the area of the original n-gon in constructing the Sierpinski n-gon, for \(n > 4\). But of course there are many points still left in the fractal. That is one reason why area is not a useful dimension for this set.
The exception is n = 4. This value of n corresponds to starting with a square and dividing the square into 4 pieces that exactly fit within the original square. In this case, \(4 \cdot r_4^2 = 1\) and no area is removed at any stage in the iteration because each iteration is still the original square.