


|
\({f_1}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{\sqrt 3 /14 } \\
{9 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_2}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{5 \sqrt 3 /14} \\
{3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_3}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{2 \sqrt 3 /7} \\
{-3/ 7} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_4}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{- \sqrt 3/14} \\
{-9/ 14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_5}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-5 \sqrt 3 /14} \\
{-3 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_6}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{-2 \sqrt 3/7} \\
{3/7} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_7}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}}\) |
scale by \(1/ \sqrt{7} \), rotate by A |
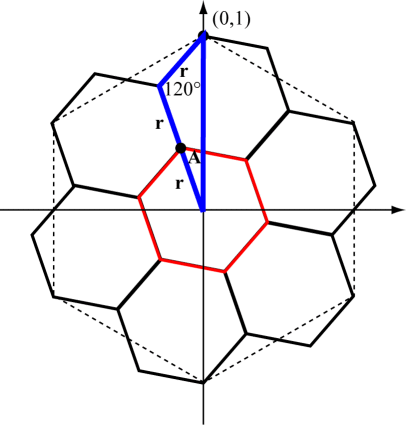
Start with a hexagon as shown in the figure above, make 7 copies scaled by a factor r, rotate them by an angle A, then translate so that six of them exactly surround the seventh (shown in red). In this case we will position the initial hexagon so that it is inscribed in the unit circle centered at the origin.
Consider the blue triangle shown in the figure. The red hexagon has been scaled by r and rotated by A. The obtuse angle is 120° by properties of regular hexagons. We can use the Law of Cosines to get
\[\begin{align} 1 &= {r^2} + {\left( 2r \right)^2} - 2 \cdot r \cdot 2r \cdot \cos {120^ \circ } \\ &= {r^2} + {4r^2} + 2r^2 = 7r^2 \\ \end{align}\]This shows that \(r = \frac{1}{\sqrt 7}\). Now by the Law of Sines,
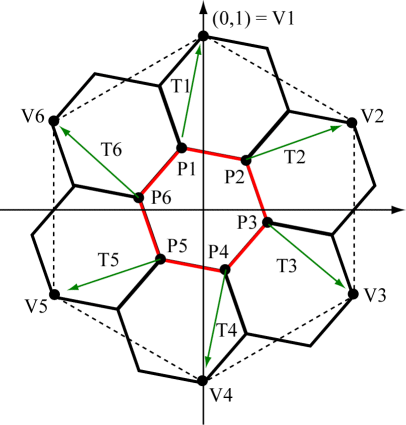
\[\begin{align} \frac{{\sin A}}{{\sin {{120}^ \circ }}} = \frac{{r}}{{1}} = \frac{1}{{\sqrt 7 }} \quad &\Rightarrow \sin A = \frac{1}{{\sqrt 7 }}\sin {120^ \circ } = \frac{{\sqrt 3 }}{{2\sqrt 7 }} \\ \\ &\Rightarrow A = \arcsin \left( {\frac{{\sqrt 3 }}{{2\sqrt 7 }}} \right) \approx {19.1066^ \circ } \\ \end{align}\]The red hexagon does not need to be translated, but each of the other 6 scaled and rotated hexagons needs to be translated so that the appropriate vertex is translated back to the corresponding vertex in the original hexagon, as shown in the figure below.
\(\sin (A) = \dfrac{{\sqrt 3 }}{{2\sqrt 7 }} = \dfrac{{\sqrt 3 \cdot \sqrt 7 }}{{14}}\)
\(\cos (A) = \sqrt {1 - {{\sin }^2}(A)} = \sqrt {1 - \dfrac{{21}}{{{{14}^2}}}} = \dfrac{{5\sqrt 7 }}{{14}}\)
To find the translation vectors, we just need to compute \({T_i} = {V_i} - {P_i} = {V_i} - M{V_i}\). This gives
\({T_1} = \left[ {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \\ \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\sqrt 3 /14} \\ {9/14} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0.12372 \\ 0.64286 \\ \end{array}} \right] \)
\({T_2} = \left[ {\begin{array}{*{20}{c}} {\sqrt 3 /2} \\ {1/2} \\ \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \\ \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\sqrt 3 /2} \\ {1/2} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {5\sqrt 3 /14} \\ {3/14} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0.61859 \\ 0.21429 \\ \end{array}} \right] \)
\({T_3} = \left[ {\begin{array}{*{20}{c}} {\sqrt 3 /2} \\ { - 1/2} \\ \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \\ \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\sqrt 3 /2} \\ { - 1/2} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {2\sqrt 3 /7} \\ { - 3/7} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0.49487 \\ -0.42857 \\ \end{array}} \right] \)
Now use symmetry to get the other three translation vectors since \({T_4} = - {T_1}\), \({T_5} = - {T_2}\), and \({T_6} = - {T_3}\).