
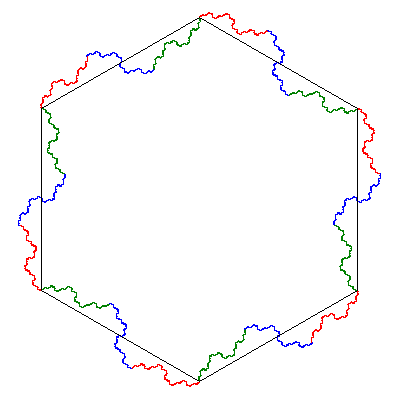
The boundary of the flowsnake can be obtained through an iterative construction that replaces the line segments forming the boundary of the hexagon with the following zigzag motif, where each of the three smaller segments have been scaled by \(1 / \sqrt 7 \).
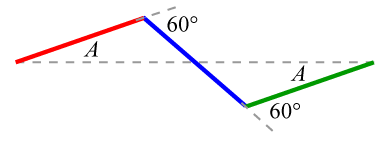
Each edge of the hexagon requires its own iterated function system based on this motif. For all of them, however, the scaling/rotation matrix for the first (red) and third (green) segments would be \[M_1 = \frac{1}{\sqrt 7}\left[ {\begin{array}{*{20}{c}} {\cos A} & { - \sin A} \\ {\sin A} & {\cos A} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.35714} & { - 0.12372} \\ {0.12372} & {0.35714} \\ \end{array}} \right]\] The middle (blue) segment is rotated by \(A-60^\circ\), so its scaling/rotation matrix would be \[M_2 = \frac{1}{\sqrt 7}\left[ {\begin{array}{*{20}{c}} {\cos (A-60^\circ)} & { - \sin (A-60^\circ)} \\ {\sin (A-60^\circ)} & {\cos (A-60^\circ)} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {2/7} & { \sqrt 3 /7} \\ {-\sqrt 3 /7} & {2/7} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {0.28571} & { 0.24744} \\ {-0.24744} & {0.28571} \\ \end{array}} \right]\]
(Recall that \(A = \arcsin \left( {\frac{{\sqrt 3 }}{{2\sqrt 7 }}} \right)\) so \(\sin(A)=\frac{\sqrt 3}{2\sqrt 7}\) and \(\cos(A)=\frac{5}{2\sqrt 7}.\))
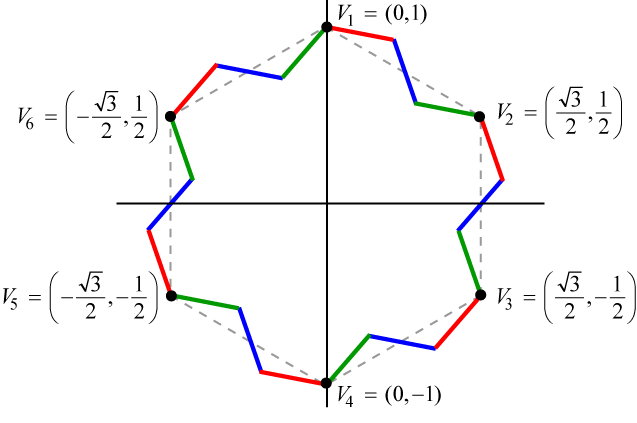
The first iteration of the motif applied to each of the edges of the hexagon inscribed in the unit circle would look like the following.
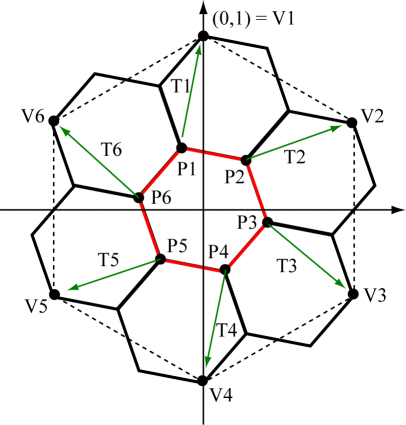
Now consider what the first iterated function system for the edge \(V_1V_2\) should do, as shown in the figure below.
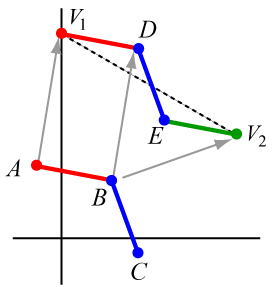
The first function in the IFS applies the scaling/rotation matrix \(M_1\) to edge \(V_1V_2\) and results in segment \(AB\), where the vertex \(V_2\) gets mapped to the point \[M_1 V_2 = \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} \sqrt{3}/2 \\ 1/2 \end{bmatrix} = \begin{bmatrix} \sqrt{3}/7 \\ 2/7 \end{bmatrix}\]
The second function in the IFS applies the scaling/rotation matrix \(M_2\) to edge \(V_1V_2\) and results in segment \(BC\), where the vertex \(V_1\) gets mapped to the point \[M_2 V_1 = \begin{bmatrix} {2/7} & { \sqrt 3 /7} \\ {-\sqrt 3 /7} & {2/7} \end{bmatrix} \begin{bmatrix} 0 \\ 1\end{bmatrix} = \begin{bmatrix} \sqrt{3}/7 \\ 2/7 \end{bmatrix}\]
This verifies that the end of the red segment really does coincide with the start of the blue segment at point B as shown in the figure above. Now each segment must be translated so that point \(A\) is translated to \(V_1\) and point \(B\) is translated to point \(D\). But the same translation vector will work for both segments, namely \[T_{11} = T_{12} = V_1 - M_1 V_1 = \begin{bmatrix} 0 \\ 1\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} 0 \\ 1\end{bmatrix} = \begin{bmatrix} \sqrt{3}/14 \\ 9/14\end{bmatrix}\]
The third function in the IFS applies the same scaling/rotation matrix \(M_1\) to edge \(V_1V_2\) as did the first function. So this results again in the segment \(AB\), but now point \(B\) needs to be translated to \(V_2\). This translation vector would therefore be \[T_{13}=V_2 - M_1 V_2 = \begin{bmatrix} \sqrt 3/2 \\ 1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} \sqrt 3/2 \\ 1/2\end{bmatrix} = \begin{bmatrix} 5\sqrt{3}/14 \\ 3/14\end{bmatrix}\]
The IFS for the boundary formed by the first edge is therefore|
\({f_{11}}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{\sqrt 3 /14} \\
{9 /14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
|
\({f_{12}}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 2/ 7} & {\sqrt 3 /7 } \\
{-\sqrt 3 /7} & { 2/ 7} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{\sqrt 3 /14} \\
{9/14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A-60 |
|
\({f_{13}}({\bf{x}}) = \left[ {\begin{array}{*{20}{c}}
{ 5/ 14} & {-\sqrt 3 /14 } \\
{\sqrt 3 /14} & { 5/ 14} \\
\end{array}} \right]{\bf{x}} + \left[ {\begin{array}{*{20}{c}}
{5\sqrt 3 /14} \\
{3/14} \\
\end{array}} \right]\) |
scale by \(1/ \sqrt{7} \), rotate by A |
\( T_{21} = V_2 - M_1 V_2 = \begin{bmatrix} \sqrt 3/2 \\ 1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} \sqrt 3/2 \\ 1/2\end{bmatrix} = \begin{bmatrix} 5\sqrt{3}/14 \\ 3/14\end{bmatrix}\)
\(T_{22} = T_{21} = \begin{bmatrix} 5\sqrt{3}/14 \\ 3/14\end{bmatrix}\)
\(T_{23} = V_3 - M_1 V_3 = \begin{bmatrix} \sqrt 3/2 \\ -1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} \sqrt 3/2 \\ -1/2\end{bmatrix} = \begin{bmatrix} 2\sqrt{3}/7 \\ -3/7\end{bmatrix}\)
\( T_{31} = V_3 - M_1 V_3 = \begin{bmatrix} \sqrt 3/2 \\ -1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} \sqrt 3/2 \\ -1/2\end{bmatrix} = \begin{bmatrix} 2\sqrt{3}/7 \\ -3/7\end{bmatrix}\)
\(T_{32} = T_{31} = \begin{bmatrix} 2\sqrt{3}/7 \\ -3/7\end{bmatrix} \)
\(T_{33} = V_4 - M_1 V_4 = \begin{bmatrix} 0 \\ -1\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} 0 \\ -1\end{bmatrix} = \begin{bmatrix} -\sqrt{3}/14 \\ -9/14\end{bmatrix}\)
\(T_{41} = V_4 - M_1 V_4 = \begin{bmatrix} 0 \\ -1\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} 0 \\ -1\end{bmatrix} = \begin{bmatrix} -\sqrt{3}/14 \\ -3/14\end{bmatrix} \)
\(T_{42} = T_{41} = \begin{bmatrix} -\sqrt{3}/14 \\ -3/14\end{bmatrix} \)
\(T_{43} = V_5 - M_1 V_5 = \begin{bmatrix} -\sqrt 3/2 \\ -1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} -\sqrt3 /7 \\ -1/2\end{bmatrix} = \begin{bmatrix} -5\sqrt{3}/14 \\ -3/14\end{bmatrix}\)
\(T_{51} = V_5 - M_1 5_2 = \begin{bmatrix} -\sqrt 3/2 \\ -1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} -\sqrt 3/2 \\ -1/2\end{bmatrix} = \begin{bmatrix} -5\sqrt{3}/14 \\ -3/14\end{bmatrix} \)
\(T_{52} = T_{51} = \begin{bmatrix} -5\sqrt{3}/14 \\ -3/14\end{bmatrix} \)
\(T_{53} = V_6 - M_1 V_6 = \begin{bmatrix} -\sqrt 3/2 \\ 1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} - \sqrt 3/2 \\ 1/2\end{bmatrix} = \begin{bmatrix} -2\sqrt{3}/7 \\ 3/7\end{bmatrix}\)
\(T_{61} = V_6 - M_1 V_6 = \begin{bmatrix} -\sqrt 3/2 \\ 1/2\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} \sqrt 3/2 \\ -1/2\end{bmatrix} = \begin{bmatrix} -2\sqrt{3}/7 \\ 3/7\end{bmatrix} \)
\(T_{32} = T_{31} = \begin{bmatrix} -2\sqrt{3}/7 \\ 3/7\end{bmatrix} \)
\(T_{33} = V_1 - M_1 V_1 = \begin{bmatrix} 0 \\ 1\end{bmatrix} - \begin{bmatrix} {5/14} & { - \sqrt 3 /14} \\ {\sqrt 3 /14} & {5/14} \end{bmatrix} \begin{bmatrix} 0 \\ 1\end{bmatrix} = \begin{bmatrix} \sqrt{3}/14 \\ 9/14\end{bmatrix}\)